Stanford公開課機器學習---week2-1.多變數線性迴歸 (Linear Regression with multiple variable)
3.多變數線性迴歸 (Linear Regression with multiple variable)
3.1 多維特徵(Multiple Features)
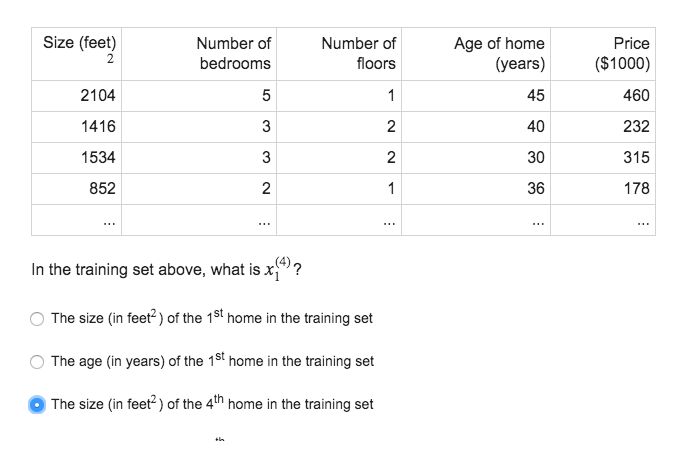
- n 代表特徵的數量
x(i) 代表第 i 個訓練例項,是特徵矩陣中的第 i 行,是一個向量(vector)。x(i)j 代表特徵矩陣中第 i 行的第 j 個特徵,也就是第 i 個訓練例項的第 j 個特徵。
多維線性方程:
hθ=θ0+θ1x+θ2x+...+θnx
這個公式中有 n+1 個引數和 n 個變數,為了使得公式能夠簡化一些,引入
多維線性方程 簡化為:
hθ=θTX
3.2 多變數梯度下降(Gradient descent for multiple variables)
cost function :
J(θ)=12m∑1m(hθ(x(i))−y(i))2
在 Octave 中,寫作: J = sum((X * theta - y).^2)/(2*m);梯度下降公式:
θj:=θj−α∂∂θjJ(θ0,θ1) =θj−α1m∑1m((hθ(x(i))−y(i))⋅x(i)j)
在 Octave 中,寫作:
t heta=theta−alpha/m∗X′∗(X∗theta−y);
3.3 特徵縮放(feature scaling)
以房價問題為例,假設我們使用兩個特徵,房屋的尺寸和房間的數量,尺寸的值為 0- 2000 平方英尺,而房間數量的值則是 0-5,繪製代價函式的等高線圖,看出影象會顯得很扁,梯度下降演算法下降的慢,而且可能來回震盪才能收斂。
mean normalization
解決的方法是嘗試將所有特徵的尺度都儘量歸一化到-1 到 1 之間。最簡單的方法是令
其中 
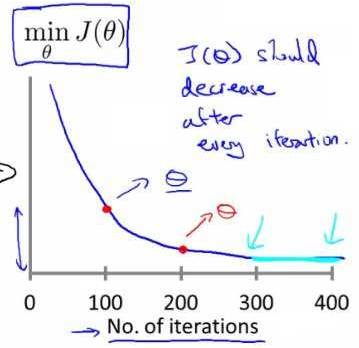
3.4 學習率(Learning rate)
- 確保梯度下降working correctly
繪製迭代次數和代價函式的圖表來觀測演算法在何時趨於收斂。下降說明正常
若增大或來回波動,可能是
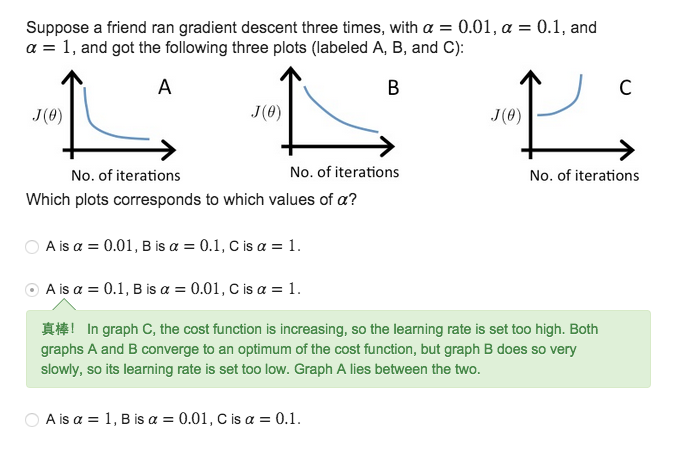
2.如何選取
先在10倍之間取,找到合適的區間後,在其中再細化為3倍左右(log)
We recommend trying values of the learning rate α on a log-scale, at multiplicative steps of about 3 times the previous value
α=…,0.001,0.01,0.1,1,…
α=…,0.001,0.03,0.01,0.03,0.1,0.3,1,…
3.5 多項式迴歸(Features and Polynomial Regression)
房價預測問題
3.多變數線性迴歸 (Linear Regression with multiple variable)
3.1 多維特徵(Multiple Features)
n 代表特徵的數量
x(i)代表第 i 個訓練例項,是特徵矩陣中的第 i 行,是一個向
1. 模型表達(Model Representation)
我們的第一個學習演算法是線性迴歸演算法,讓我們通過一個例子來開始。這個例子用來預測住房價格,我們使用一個數據集,該資料集包含俄勒岡州波特蘭市的住房價格。在這裡,我要根據不同房屋尺寸所售出的價格,畫出我的資料集:
我們來看這個資料集,如果你有一個朋 學習筆記 機器 增加 都是 維度 能夠 因此 表示 轉置 我們探討了單變量/特征的回歸模型,現在我們對房價模型增加更多的特征,例如房間數樓層等,構成一個含有多個變量的模型,模型中的特征為(??1, ??1, . . . , ????)。
增添更多特征後,我們引入一
1多變數線性迴歸
1.1 回顧單變數線性迴歸
訓練集提出:
Training set of housing prise 以房屋價格為例
Size in feet(x)
Price in 1000’s (y)
2104
460
1416
2
本篇主要講的是多變數的線性迴歸,從表示式的構建到矩陣的表示方法,再到損失函式和梯度下降求解方法,再到特徵的縮放標準化,梯度下降的自動收斂和學習率調整,特徵的常用構造方法、多維融合、高次項、平方根,最後基於正規方程的求解。
在平時遇到的一些問題,更多的是多特徵的
多變數的表示方法
多元線性迴歸中的損失
機器學習練習1——單變數線性迴歸代價函式:梯度下降練習1資料集代價函式梯度下降法視覺化J
單變數線性迴歸
代價函式:
梯度下降
練習1
資料集
X代表poplation,y代表profits
資料集的視覺化
function plotData(x,
在統計學中,線性迴歸(英語:linear regression)是利用稱為線性迴歸方程的最小二乘函式對一個或多個自變數和因變數之間關係進行建模的一種迴歸分析。這種函式是一個或多個稱為迴歸係數的模型引數的線性組合。只有一個自變數的情況稱為簡單迴歸,大於一個自變數情況的叫做多元迴歸(multi
吳恩達(Andrew Ng)在 Coursera 上開設的機器學習入門課《Machine Learning》:
目錄
一、引言
一、引言
1.1、機器學習(Machine Learni
目錄
0. 前言
1. 假設函式(Hypothesis)
2. 標準線性迴歸
2.1. 代價函式(Cost Function)
2.2. 梯度下降(Gradient Descent)
2.3. 特徵縮放(Feat
線性迴歸演算法
1 簡單線性迴歸(Simple Liner Regression)
解決迴歸問題
思想簡答,容易實現
許多強大的非線性模型的基礎
結果具有很好的可解釋性
蘊含機器學習中的很多重要思想
1.1 什麼是線性迴歸演算法?
需要下載一個data:auto-mpg.data
第一步:顯示資料集圖
import pandas as pd
import matplotlib.pyplot as plt
columns = ["mpg","cylinders","displacement","horsepowe
線性學習中最基礎的迴歸之一,本文從線性迴歸的數學假設,公式推導,模型演算法以及實際程式碼執行幾方面對這一回歸進行全面的剖析~
一:線性迴歸的數學假設
1.假設輸入的X和Y是線性關係,預測的y與X通過線性方程建立機器學習模型
2.輸入的Y和X之間滿足方程Y= θ
(一)認識迴歸
迴歸是統計學中最有力的工具之一。機器學習監督學習演算法分為分類演算法和迴歸演算法兩種,其實就是根據類別標籤分佈型別為離散型、連續性而定義的。顧名思義,分類演算法用於離散型分佈預測,如前
引言
如果要將極大似然估計應用到線性迴歸模型中,模型的複雜度會被兩個因素所控制:基函式的數目(的維數)和樣本的數目。儘管為對數極大似然估計加上一個正則項(或者是引數的先驗分佈),在一定程度上可以限制模型的複雜度,防止過擬合,但基函式的選擇對模型的效能仍然起著決定性的作用。
第一章講述了基本的機器學習的概念以及分類,這裡從單變數的線性迴歸入手,吳恩達講解了機器學習中的幾個重要因素,如模型、損失函式、優化方法等
首先以房價預測入手:
房子的面積
每平米的房價
2104
460
1416
232
1534
315
852
178
其中:
m 為
The Hypothesis Function
we will be trying out various values of θ0 and θ1 to try to find values which provide the best possibl
內容來自Andrew老師課程Machine Learning的第二章內容的Multivariate Linear Regression部分。
一、Multiple Features(多特徵)
1、名詞
(1)mm:樣本的數量,上例中m=4
(2)nn
一、概念形式化
輸入:x
輸出:y
目標函式:F:x → y
資料:(x1, y1), (x2, y2), …, (xN, yN)
假設函式:g:x → y
假設集:H={h}, G∈H
(假設集有助於理解是否用這個演算法及用這個演 繼續 例子 產生 成本 log repr 概率 .cn 成了
如上圖所示,如果用邏輯回歸來解決這個問題,首先需要構造一個包含很多非線性項的邏輯回歸函數g(x)。這裏g仍是s型函數(即 )。我們能讓函數包含很多像這的多項式,當多項式足夠多時,那麽你也許能夠得到可以 如何 work 單元 pre 結果 mda s函數 額外 權重 神經網絡是在模仿大腦中的神經元或者神經網絡時發明的。因此,要解釋如何表示模型假設,我們先來看單個神經元在大腦中是什麽樣的。如下圖,我們的大腦中充滿了神經元,神經元是大腦中的細胞,其中有兩點值得我們註意,一是神經
已知x1=frontage(臨街寬度),x2=depth(縱向深度),則相關推薦
Stanford公開課機器學習---week2-1.多變數線性迴歸 (Linear Regression with multiple variable)
機器學習之單變數線性迴歸(Linear Regression with One Variable)
吳恩達機器學習筆記8-多變量線性回歸(Linear Regression with Multiple Variables)--多維特征
#機器學習筆記01#多變數線性迴歸
吳恩達機器學習筆記 —— 5 多變數線性迴歸
吳恩達機器學習練習1——單變數線性迴歸
機器學習入門之單變數線性迴歸(上)——梯度下降法
吳恩達(Andrew Ng)《機器學習》課程筆記(1)第1周——機器學習簡介,單變數線性迴歸
機器學習實戰(七)線性迴歸(Linear Regression)
機器學習筆記——線性迴歸(Linear Regression)
用python來實現機器學習(一):線性迴歸(linear regression)
機器學習之線性迴歸(Linear Regression)
機器學習經典演算法詳解及Python實現--線性迴歸(Linear Regression)演算法
【機器學習】貝葉斯線性迴歸(最大後驗估計+高斯先驗)
吳恩達機器學習筆記 —— 2 單變數線性迴歸
吳恩達Coursera機器學習課程筆記-單變數線性迴歸
Machine Learning第二講[多變數線性迴歸] --(一)多變數線性迴歸
【機器學習】加州理工學院公開課——機器學習與資料探勘 1.學習問題
斯坦福大學公開課機器學習:Neural Networks,representation: non-linear hypotheses(為什麽需要做非線性分類器)
斯坦福大學公開課機器學習:Neural network-model representation(神經網絡模型及神經單元的理解)