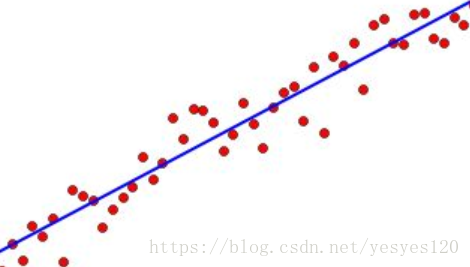
如何使用線性代數實現最小二乘法擬合曲線

阿新 • • 發佈：2019-02-03

也許在我們讀高中的時候，就知道在數學的世界裡，有一種直線擬合的方式：最小二乘法。它是一種數學優化技術，原理是通過最小化誤差的平方和尋找資料的最佳函式匹配。

比如研究x和y之間的關係，假設我們擁有的資料是 ${\color{Red} (x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3}),(x_{4},y_{4}),...,(x_{m-1},y_{m-1}),(x_{m},y_{m}),}$ 將這些資料描繪在x-y直角座標系中，發現這些點並沒有能夠連線成一條直線。

但趨勢近似一條曲線，這時可以假設這條曲線為： ${\color{Red} \hat{y}=\hat{k}x+b}$ 。

根據最小二乘的原理，使 ${\color{Red} \sum_{i=1}^{m}(y_{i}-\hat{y_{i}})^{2}}$ 即 ${\color{Red} \sum_{i=1}^{m}(y_{i}-\hat k{x_{i}-b})^{2}}$ 最小化,可以得到 $\hat{k}$ 值，再根據直線過點 ${\color{Red} (\bar{x},\bar{y})}$ 得出b的值。 $\color{Red} \bar{x}$ 為橫座標的平均值， $\color{Red} \bar{y}$ 為縱座標的平均值。

其中， ${\color{Red} \hat{k}=\frac{\sum_{i=1}^{m}xy-\frac{1}{m}\sum_{i=1}^{m}x*\sum_{i=1}^{m}y}{\sum_{i=1}^{m}x^{2}-\frac{1}{m}(\sum_{i=1}^{m}x)^{2}}}$ , ${\color{Red}b= \hat{y}-\hat{k}x}$ 。

其實最小二乘法不僅可以擬合直線（一次），還可以擬合曲線（≥2次）。

在溫習了高中所學的最小二乘法後，讓我們使用大學裡線性代數的知識，進行擬合吧。

Ax=b，A是m*n型的矩陣其中m>n，A列滿秩，那麼Ax=b可能有解，也可能無解。

如果Ax=b有解，因為列滿秩，容易得知x的解是唯一的，其實可以想象成空間裡投影，就是b在A的列空間上C（A）裡投影是唯一的；

如果Ax=b無解，說明b ∉ C（A），那麼我們把問題轉化一下：求 $\hat{x}$ ，使得A $\hat{x}$ 與b之間的距離最小，也就是Min ${\color{Red} ||b-A\hat{x}||}$

這時我們需要一點空間想象的能力，所要求的 $\hat{x}$ ，無非就是向量b在C（A）這個空間上的投影點，因為只有在這種情況下，||b-A $\hat{x}$ ||才是最小。

我們來看一個點在直線上投影的例子：

如圖，我們要求b在a上的投影向量p，只要稍微懂點高中數學的向量知識，我們可以得到下面兩個式子：

①p+e=b，e⊥a

②p=ta（t∈R）

因為e⊥a，所以 $a\cdot (b-ta)=0$ ，也就是 $a^{T}(b-ta)=0$ ，所以 $t=\frac{a^{T}b}{a^{T}a}(a\neq 0)$

那麼b在a上的投影向量為 $p=(\frac{a^{T}b}{a^{T}a})a$

又因為 $(a^{T}b)a=a(a^{T}b)=(aa^{T})b$

所以投影向量又可以寫成 $p=(\frac{aa^{T}}{a^{T}a})b$

習慣上，我們習慣將 $S=\frac{aa^{T}}{a^{T}a}$ 稱為投影矩陣，比如對任意b∈ $R^{2}$ ，Sb是b在a上的投影向量。

我們會發現一個有趣的性質， $S^{2}=S,S^{T}=S$ ，其實很好理解，Sb是指b在a上的投影向量，那麼 $S^{2}b$ 則是指b在a上投影一次後的投影，再投影一次，Sb和 $S^{2}b$ 無疑是相等的，所以 $S^{2}=S$ ，根據 $S^{2}=S$ 容易得出 $S^{T}=S$ ，此處不進行推導。