拉格朗日乘子法是一種尋找多元函式在一組約束下的極值方法,通過引入拉格朗日乘子,可將有m個變數和n個約束條件的最優化問題轉化為具有m+n個變數的無約束優化問題。在介紹拉格朗日乘子法之前,先簡要的介紹一些前置知識,然後就拉格朗日乘子法談一下自己的理解。
一 前置知識
1.梯度
梯度是一個與方向導數有關的概念,它是一個向量。在二元函式的情形,設函式f(x,y)在平面區域D內具有一階連續偏導,則對於每一點P(x0,y0)∈D,都可以定義出一個向量:fx(x0,y0)i+fy(x0,y0)j ,稱該向量為函式f(x,y)在點P(x0,y0)
的梯度。並記作grad f(x0,y0)
或者∇f(x0,y0),即 grad f(x0,y0)
= ∇f(x0,y0) = fx(x0,y0)i+fy(x0,y0)j 。
再來看看梯度和方向導數的關係:如果函式f(x,y)在P(x0,y0)點可微,el = (cosα,cosβ)是與方向L同向的單位向量,則∂f/∂L|(x0,y0) = fx(x0,y0)cosα+fy(x0,y0)cosβ = grad f(x0,y0).el = |grad f(x0,y0)|.cosθ ,其中θ表示的梯度與el 的夾角。由此可知,當θ = 0時,el 與梯度的方向相同時,此時方向導數最大,函式f(x,y)增長最快;當θ = π時,el 與梯度的方向相反時,此時方向導數最小且為負,函式f(x,y)減小最快。
2.等高線(等值線)
通常來說,二元函式 z = f(x,y)在幾何上表示一個曲面,這個曲面被平面 z = c(c為常數)所截得的曲線L的方程為:

這是一條空間曲線,這條曲線L在xOy平面上的投影是一條平面曲線L*,它在xOy平面直角座標系中的方程為:f(x,y) = c .對於曲線L*上的一切點,已給函式的函式值都是c,所以我們稱平面曲線L*為函式z = f(x,y)的等值線(等高線)。再來看看等高線的一些性質:
若fx,fy不同時為零,則等高線 f(x,y) = c上任一點P(x0,y0)處的一個單位法向量為:
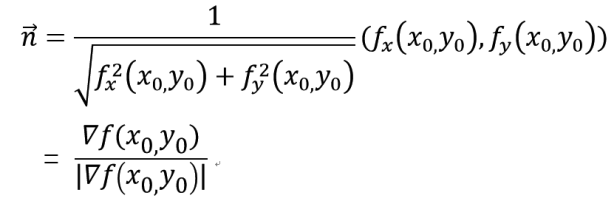
這表明函式f(x,y)在一點(x0,y0)的梯度∇f(x0,y0)的方向就是等高線f(x,y) = c在這點的法向量的方向,而梯度的模|∇f(x0,y0)|就是沿這個法線方向的方向導數∂f/∂n,於是有:
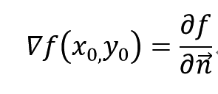
二 拉格朗日乘子法
1.等式約束
首先看一下什麼是拉格朗日乘子法,已知一個問題:
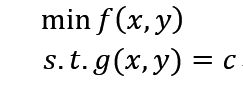
要求f(x,y)在g(x,y)=c的前提下的最小值,我們可以構造一個函式L(λ,x,y) = f(x,y) + λ(g(x,y) - c),其中λ(λ不等於0)稱為拉格朗日乘子,而函式L(λ,x)稱為拉格朗日函式。通過拉格朗日函式對各個變數求導,令其為零,可以求得候選值集合,然後驗證求得最優值。這就是拉格朗日乘子法。那麼拉格朗日乘子法為什麼是合理的?下面分別從幾何和代數兩方面解釋下自己對其的一些見解:
(1)從幾何的角度
先來看一幅圖:
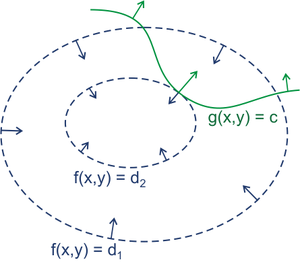
圖中的虛線表示f(x,y)的等高線,如果滿足g(x,y)=c這個約束,必然是等高線與g(x,y)=c這條曲線的交點;假設g(x)與等高線相交,交點就是同時滿足等式約束條件和目標函式的可行域的值,但並不是最優值,因為相交意味著肯定還存在其它的等高線在該條等高線的內部或者外部,使得新的等高線與目標函式的交點的值更大或者更小,只有到等高線與目標函式的曲線相切的時候,才可能取得最優值。假設該切點為P(x0,y0),則f(x,y)在p點的梯度必然垂直於其在該點處的法向量(前面已經說過),又由於p點是曲線g(x,y)=c的切點,故曲線在p點的法向量平行於等高線在p點法向量(也可以看做兩條曲線在該點有相同的法向量),故g(x,y)=c的梯度必然也垂直於它在p點的法向量。所以最優值必須滿足:∇f(x,y) = λ* ∇(g(x)-c),λ是常數且不等於0,表示左右兩邊平行。這個等式就是L(λ,x)對引數分別求偏導的結果,即:
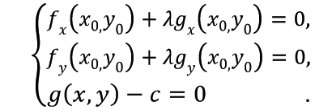
也就是說滿足∇f(x,y) = λ* ∇(g(x)-c)的點必然是式子min L(λ,x) = f(x,y) + λ(g(x,y) - c)的解,所以min L(λ,x) = f(x,y) + λ(g(x,y) - c)這個式子與原問題是等價的(可以先簡單的認為g(x,y) - c = 0造成的)。
(2)從代數的角度
先來看一下z = f(x,y)在條件g(x,y) = c下取得極值的必要條件。
如果z=f(x,y)在(x0.y0)處取得所求的極值,那麼有 g(x0,y0) = c,假定在(x0,y0)的某一領域內f(x,y)與g(x,y) = c均有一階段連續偏導(對於凸函式很顯然是成立的)並且gy(x0,y0)≠0.由隱函式的存在定理可知方程g(x,y)=c能夠確定一個連續且具有連續偏導的函式y = μ(x),將其帶入z= f(x,y)中可以得到一個變數x的函式:z = f[x,μ(x)].
於是z=f(x,y)在x=x0處取得極值,相當於z = f[x,μ(x)]在x=x0處取得極值,又由一元可導函式取得極值的必要條件可知:
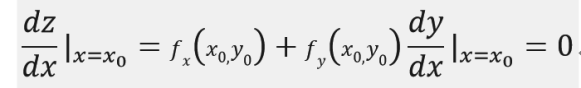
而又由y = μ(x)用隱函式求導公式,有

將以上兩式結合可得,
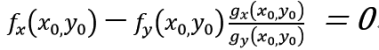
上式與g(x0,y0)=c 就是函式z=f(x,y)在g(x,y)=c的條件下取得極值的必要條件。如果令:
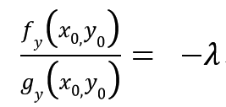
上述的必要條件就變為
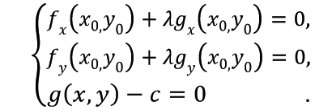
同從幾何角度推出的結論一致。
綜上所述,對於問題

(x可以為一個向量,也可以為一個標量)
等價於求
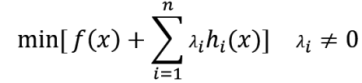
三 KKT條件
1.關於不等式約束
上述問題中講述的都是約束條件為等式的情況,對於約束條件為不等式的情況,通常引入KKT條件(在不等式約束下,函式求極值的必要條件)來解決,具體如下:
對於問題
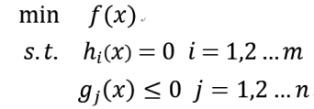
我們也引入拉格朗日函式
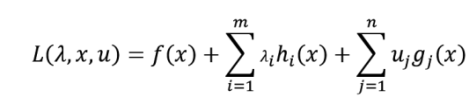
其中μj≥0。
再看一個關於x的函式:
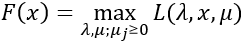
而實際上F(x)可以看做是f(x)的另一種表達形式;由於hi(x)=0,所以拉格朗日函式中的第二項為0;又由於gj(x) ≤ 0且μj ≥ 0,所以μjgj(X) ≤ 0,所以只有μjgj(X) = 0時L取到最大值;因此F(x)在滿足約束條件時就是f(x)。由此,目標函式可以表述為如下的形式:
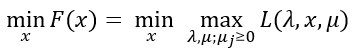
我們稱這個式子為原問題。並定義原問題的最優值為P*。
然後再看關於λ和μ的一個式子:

考慮該式子的極大化:
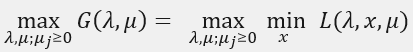
我們稱這個式子為原問題的對偶問題。並定義對偶問題的最優值為d*。
(關於拉格朗日的對偶性,可參考李航《統計學習方法》中的附錄部分,或者參考部落格:http://blog.pluskid.org/?p=702)
關於對偶性問題,通常分為弱對偶性和強對偶性:
(1)考慮到原問題和對偶問題的最優值P*和d*,如果d* ≤ P*,則稱“弱對偶性”成立。
(2)如果d* = P*,則稱“強對偶性”成立。
通常情況下,強對偶性並不成立;但是當原問題和對偶問題滿足以下條件時,則滿足強對偶性。
(1)f(x)和gj(x)是凸函式。
(2)hi(x)是仿射函式。
(3)不等式約束gj(x)是嚴格可行的,即存在x,對所有j有gj(x) < 0 。
以上三個條件也稱為Slater條件。如果滿足Slater條件,即原問題和對偶問題滿足強對偶性,則x*和λ*、μ*分別為原問題和對偶問題的最優解的充要條件是x0和λ0、μ0滿足下面的條件:
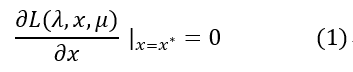
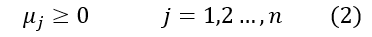
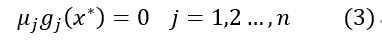
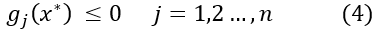
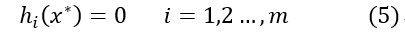
以上五個條件就是所謂的Karush-Kuhn-Tucher(KKT)條件。下面是關於這幾個條件的簡單闡述:
對於第一個條件,由於原問題和對偶問題滿足強對偶性,所以
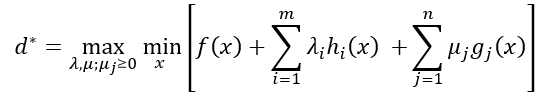
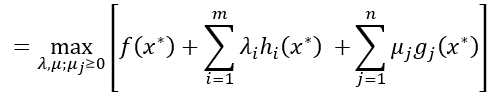
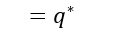
即關於x的函式:
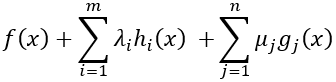
在x*處取到了極值,由費馬引理可知,該函式在x*處的偏導數為0,即:
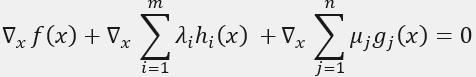
也就是條件(1)。該式子說明f(x)在極值點x*處的梯度是各個hi(x*)和gj(x*)的線性組合。
對於第二個條件,時在定義拉格朗日函式時的約束條件。
對於第三個條件,在定義F(x)時就已經體現了,由於:
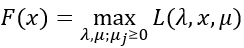
因為μjgj(x)≤0,要使得L最大,只有μjgj(x) = 0時滿足。所以產生了第三個條件。
對於第四、五個條件,是原問題的自帶的約束條件。
當原問題和對偶問題不滿足強對偶性時,KKT條件是使一組解成為最優解的必要條件,即在不等式約束下,函式求極值的必要條件。可以把KKT條件看成是拉格朗日乘子法的泛化。