The Essence of Quantum Mechanics Part 1: Measurement and Spin

Despite what you may have heard, quantum physics isn’t really a difficult subject to understand. Like all physical theories, it ultimately consists of nothing more than a collection of rules and mathematical formulas for drawing conclusions from those rules. The only thing that separates quantum physics from the physics of everyday experience is that the rules can seem counterintuitive or unusual or even arbitrary. My aim with this series, “The Essence of Quantum Mechanics” is not necessarily to teach you quantum physics in detail, but to convince you that it can be understood and to explain its most basic components.

In this first article, we will tackle the question of what it means to measure the state of a quantum system.

Measurement

We take for granted in classical physics that we can perfectly know the state of a physical system. If only it were possible to create a sufficiently accurate ruler, thermometer, or scale, then it would be possible to know the length, temperature, or mass of a system to arbitrarily high precision. We also take for granted that the state of the system exists independent of our efforts to measure it. If we measure the dimensions of a room, we take for granted that the room will continue to have the same dimensions even after we stop measuring, and if the room’s dimensions were to ever change then this change would be the result of a knowable physical process (thermal expansion of the house, or a builder renovating the room). And furthermore, even when we are not measuring the room’s length and width, we take for granted that at any time it has only one value for its length and only one value for its width.

These are the assumptions about the world that we have to leave behind when we start doing quantum physics. It’s not merely that precise measurements of quantum systems are impossible in practice, but rather that a “precise measurement” of a quantum system’s state is no longer physically meaningful. What we say instead is that a quantum system exists in a superposition of states: the system is in all

One of the best examples of this is the famous Stern-Gerlach experiment.

The Stern-Gerlach experiment

This experiment was performed by Otto Stern and Walter Gerlach in 1922. A beam of neutral silver atoms was produced in an oven and passed through an inhomogeneous magnetic field, and it was observed that the beam was split into two, with one beam deflected in the direction of the magnetic field and the other deflected in the direction opposite to the magnetic field.

Some atoms are deflected exactly parallel to the magnetic field and some are deflected exactly antiparallel, and this is the behavior that we would expect if each atom was a pure magnetic dipole (think of a bar magnet) with magnetic moment μ. (You can think of the moment as being what tells the magnet itself how to react when exposed to an external magnetic field). The potential energy of the silver atoms interacting with the magnetic field will be given by U=-μ·B so that the force on the particle is F= ∇(μ·B). The magnetic field is very close to uniform in the x and y directions so the force is in the z-direction and its magnitude is given by

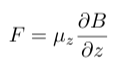
Where μz is the component of the magnetic moment of the atom in the z direction (aligned with the magnetic field). For a charged particle orbiting in a circle (such as an electron orbiting the nucleus of an atom), we know from classical electromagnetic theory that there are two contributors to the magnetic moment. The first is a term associated with the orbital angular momentum of the charged particle around the center of the force (in this case the nucleus) :

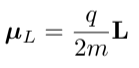
And the second is a term associated with the intrinsic angular momentum, or spin, of the charged particle about its own axis:

In the second formula, g is a dimensionless quantity called the gyromagnetic ratio, its value is approximately 2.0023. Computing this is very difficult and is more of a problem in electromagnetic theory so we won’t do it here. We should be careful when talking about electrons in atoms. Electrons do not orbit around the nucleus like planets around the Sun, nor do they spin like little tops around their own axes. They just act like they do for the purposes of the atom’s magnetic interactions, in the sense that the atom’s magnetic moment turns out to be exactly what we would expect if that were truly the case. The terminology is an artifact from the earliest days of atomic physics and unfortunately we’re stuck with it.

The choice of silver atoms for the experiment was not an accident. The electron configuration of silver is 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶4d¹⁰5s¹. The first 46 of the atom’s electrons are in closed shells, and closed shells have no net angular momentum. Furthermore, the Pauli exclusion principle tells us that the spins of the electrons in closed shells will cancel out. This means that the only electron that is able to contribute to the magnetic moment is the single electron in the 5s orbital. And since s orbitals do not have orbital angular momentum, the only factor contributing to the silver atom’s total magnetic moment is the spin of the single electron in the 5s orbital.

Classically, we would expect that the magnetic moments of the atoms would be randomly distributed, and the result of the beam passing through the magnetic field would be a “spray” onto the screen reflecting their random orientations and magnitudes. But instead, the beam is split cleanly into two.

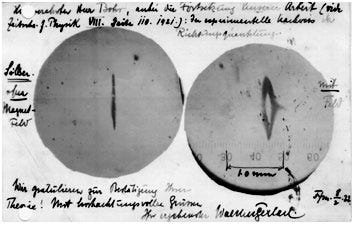
The above image depicts the slides from the original experiment performed in 1922. The silver atoms passed through the apparatus and formed a layer on the slides. The left slide was from before the magnetic field was switched on. The reason that there aren’t two perfect dots is that the beam was collimated by passing it through a narrow rectangular slit, although modern replications of the experiment have corrected this. Nonetheless, the split (of only about 0.2 mm) is clearly visible, and at the center of the split it is clear that two distinct beams were hitting the slide. What this suggests is that the spins of the electrons can take only two possible values, which were determined experimentally to be ±ħ/2 = 3.29×10^(-16) eVs (electron volt seconds). The spin is always measured with respect to a particular direction. Conventionally, unless we specify a direction, we mean in the z-direction, so that we say “Spin up/down in the z-direction.” In what follows, any time I say “Spin up/down in whichever direction” or “Spin z+/-”, I mean that the numerical value of the spin is +/- ħ/2

These resultes would be shocking enough, but things get even more interesting when we start putting Stern-Gerlach apparatuses in sequence with each other. Let’s start by measuring the spin twice in the z-direction.

We pass 1000 electrons into the first apparatus and measure their spin in the z-direction, and then send the electrons with spin up to the upper apparatus and the electrons with spin down to the lower one. We make sure that the sample contains randomly electrons with randomly distributed states. In the original experiment, this was done by using a very hot vapor of silver atoms: the electrons were their 5s valence electrons and thermal effects due to the high heat removed any possible biases in the sample.

After performing the experiment a large number of times, the result is intuitively exactly what we would expect. Half of the electrons are spin up and half are spin down. Furthermore, measuring the z component of the spin a second time does not change the spin the states, which also tracks with what we would classically expect.

Now let’s measure the z-component and then the x-component.

The effect of the left apparatus is to prepare two beams of electrons, a beam of electrons all of which have spin z+ and another beam of electrons all of which have spin z-. What we find is that this preparation has no effect at all on the component of the spin in the x direction. This might seem suspicious but it does not immediately seem to conflict with our classical intuition.

Now let’s see what happens when we measure the z component, then the x component, and then the z component again.

Now that’s different. When we measure the component of the spin along the z direction after measuring the x component, we see that the electron seems to “forget” its previous value of the z component of the spin. Repeatedly measuring the spin along one axis doesn’t change the result, but the instant we try to measure it on another axis, the prepared state is destroyed.

When this happens, we say that the component of the spin in the z direction and the component of the spin in the x direction are incompatible observables: it is not possible to know both of their values at the same time. If we know that an electron has spin z+ or z- then all we can say about the x-component is that a measurement will return either spin x+ or x- with 50/50 probability.

How can we formalize these ideas?

Bracket notation

In classical mechanics a system is specified by its generalized coordinates and their associated momenta. For example, the state of a system consisting of a point particle moving along the x axis can be completely specified by the pair (x(t), p(t)), which tell you the position and momentum at any time. In quantum mechanics, a system is specified by its wave function. For continuous quantum systems, such as an electron in a hydrogen atom, the wave function may be written as ψ(r, t), and the square of the absolute value of this wave function |ψ(r, t)|² gives the probability of finding the electron at point r at time t. For discrete systems, such as the spin of an electron, we can represent the wave function as a ket vector: ∣ψ⟩ = α∣+⟩ + β∣-⟩. The vector ∣+⟩ represents spin z+ and ∣-⟩ represents spin z-. For spin in the other directions, we include a subscript x or y as appropriate. When the spin is measured, we obtain spin up with probability α² and spin down with probability β². We say that ∣ψ⟩ is a superposition of the so-called basis states ∣+⟩ and ∣-⟩.

The probability that a system prepared in state ∣ψ⟩ willbe measured to be in state ∣φ⟩ is |⟨φ∣ψ⟩|². A vector ⟨ψ∣ is called a bra vector (combined, they’re meant to say “bracket”). The bra ⟨ψ∣ is called the dual vector of the ket ∣ψ⟩. It is obtained by first transposing the column vector representation of ∣ψ⟩ and then complex conjugating its elements. For example:

If a system is in ∣ψ⟩ then obviously it is in state ∣ψ⟩ with probability one. Therefore we have the rule |⟨ψ∣ψ⟩|² =1 so ⟨ψ∣ψ⟩ = 1 . If a system is known to be in a basis state, such as ∣+⟩, then the probability that it is in another basis state like∣-⟩ is zero, so we also have the rule ⟨+∣-⟩ = ⟨-∣+⟩ = 0. Combined, these two rules are said to constitute the orthonormality property. This is the reason for the 1/√2 above, it’s called a normalization constant, and it ensures that the state vector has unit magnitude. Let’s see exactly where it comes from. Given ∣ψ⟩ = A(∣+⟩ + i∣-⟩), the ket vector form of the column vector above, find A such that ∣ψ⟩ is normalized, ie, has unit magnitude.

Now let’s do another example just to further build our familiarity with the bracket notation. Consider the state ∣ψ⟩ = (4/5)∣+⟩ + (3i/5)∣-⟩. What are the possible results of measuring the spin component along the z axis and with what probabilities do they occur?

The first step would usually be to normalize the state vector, but you can check that the ket is already normalized, so we can skip that. The obvious first part is “What are the possible results of the measurement?” Spin is quantized and its only possible values are +ħ/2 and -ħ/2. What about the probabilities? We just use the algorithm that we’ve already established.

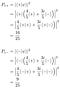
So now that we have some basic familiarity with the mathematical machinery, we’re now ready to answer the question of what’s happening to the electrons in the Stern-Gerlach experiment to make them “forget” the z component of their spin. Suppose that the first Stern-Gerlach apparatus has prepared a beam of electrons in the spin up state, so ∣ψ⟩ = ∣+⟩. To find the probability that the next apparatus will find the electron’s spin to be up in the x direction, we just carry out the same algorithm:

Before we can continue, we need to represent both the bra and the ket in the spin-z basis. The vector ∣+⟩ can be read to mean “The electron’s spin is up in the z basis.” In the next article when we talk about operators, we’ll explain what this means, and also how to show that:

So we can now compute the probability that the electron will be spin up in the x direction:

And since the probabilities add to 1, the probability that the electron will be spin down in the x direction will also be 1/2. The result will be exactly the same if the apparatus is fed an electron in the ∣-⟩ state. We can therefore conclude that if the electron is known to be in the ∣+⟩ or ∣-⟩ state then the electron must have a 50/50 probability of being spin up or down in the x direction. Now suppose that the electron has just left the Stern-Gerlach apparatus with its spin state in the x direction having been measured as spin up. When it’s fed through a Stern-Gerlach apparatus that measures the z-component, what is the probability that the electron is still spin-up? The calculation is exactly the same as above:

This tracks with the experimental results from before: The particle has no “memory” of whether it was spin z+ or spin z-. We destroyed that piece of information when we measured the x component of the spin, and there is no way to recover it. We can never know the complete state of the electron’s spin, we can only ever know probabilities, because knowledge of any one of its components precludes knowledge of the others.

This is an example of what is meant when we say that observing a quantum mechanical system changes the system. A similar reasoning will also come up later when we talk about Heisenberg’s Uncertainty Principle: Just as the spin components in the x and z directions are incompatible (ie cannot be both known at the same time), so too are position and momentum. As your knowledge of position becomes more precise, your knowledge of momentum becomes much less so. An important difference is that position and momentum are continuous and spin is discrete, but nonetheless it’s a frame of mind that you need to get yourself into.

This is why I chose this particular subject to start out the series. My intention isn’t to teach you how to do quantum physics, but rather how to think about it. And to do that, the first thing that you need to do is get your head around the ways that quantum physics is so different from the classical physics of every day life.