本篇將依據《統計自然語言處理》（宗成慶），重新梳理統計學習相關理論知識，相關概率論與梳理統計的課本不再列出來，可以找任意相關的課本復（預）習。

概率

概率是表示事件發生的可能性，將隨機試驗中的事件映射到實數域。用$P(A)$表示事件A的概率，$\Omega$表示試驗的樣本空間（所有可能發生的事件），則概率滿足：

1. 非負性：$P(A) \geq 0$
2. 規範性：$P(\Omega) = 1$
3. 可列可加性：對於可列個事件$A_1,A_2,...$，如果事件兩兩互不相容($A_i \bigcap A_j = \varnothing, \forall i \neq j$)，則有$P(\bigcup_{i} A_i) = \sum_{i} P(A_i)$

獨立

事件A 和B獨立等價於$P(AB)=P(A)P(B)$

條件概率

$$P(A|B) = \frac {P(A \bigcap B)} {P(B)} $$

$$P(A \bigcap B) = P(B)P(A|B) = P(A)P(B|A) $$

一般地，

$$P(A_1 \bigcap \cdot \cdot \cdot \bigcap A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1 \bigcap A_2) \cdot \cdot \cdot P(A_n|A_1 \bigcap A_2 \bigcap \cdot \cdot \cdot A_{n-1})$$

條件概率同樣具有概率的三個性質

1. 非負性：$P(A|B) \geq 0$
2. 規範性：$P(\Omega | B) = 1$
3. 可列可加性：如果事件$A_1,A_2,...$兩兩不相容，則$P(\sum_{i} A_i | B) = \sum_{i} P(A_i | B)$

條件獨立

如果$A_1,A_2$關於B條件獨立，當且僅當$P(A_1,A_2 |B)=P(A_1 | B)P(A_2 | B)$

貝葉斯法則

根據條件概率有

$P(B|A)=\frac {P(BA)} {P(A)} = \frac {P(A|B)P(B)} {P(A)}$

比如應用貝葉斯理論到分類問題中，假設要求已知一個特征A發生的條件下，分類為B的概率，則可以統計樣本中特征A出現的頻率（用來估計$P(A)$），並統計樣本中分類為B的那些樣本中特征為A的頻率（用來估計$P(A|B)$），於是分別計算特征A的條件下各個分類的條件概率，值最大的那個分類就是最終特征A所屬的分類，而計算這些條件概率時，P(A)可以看作常數，所以

$$arg \max_{B} \frac {P(A|B)P(B)} {P(A)} = arg \max_{B} P(A|B)P(B) $$

根據乘法規則，

$$P(A \bigcap B) = P(A|B)P(B)$$

$$P(A \bigcap \overline B) = P(A| \overline B)P(\overline B)$$

於是有，

$$P(A) = P(A \bigcap B) + P(A \bigcap \overline B) = P(A|B)P(B) + P(A| \overline B)P(\overline B) $$

一般地，假設B是樣本空間$\Omega$的一個劃分，$\sum_{i} B_i = \Omega$，如果$A \subseteq \Omega$，即$A=\sum_{i} AB_i$，那麽

$$P(A) = \sum_{i} P(AB_i) = \sum_{i} P(A|B_i)P(B_i)$$

上式稱為全概率公式

如果$P(A) > 0$，那麽

$$P(B_j | A) = \frac {P(A|B_j)P(B_j)} {P(A)} = \frac {P(A|B_j)P(B_j)} {\sum_{i} P(A|B_i)P(B_i)} $$

聯合概率分布和條件概率分布

$(X_1,X_2)$是一個二維離散隨機向量（約定大寫表示隨機變量，小寫為隨機變量的一個取值），則聯合概率分布

$$p_{ij} = P(X_1=a_i,X_2=b_j) $$

條件概率分布為

$$P(X_1 = a_i | X_2 = b_j) = \frac {P(X_1=a_i,X_2=b_j)} {P(X_2=b_j)} = \frac {p_{ij}} {P(X_2=b_j)} $$

由於$P(X_2=b_j) = \sum_{k} p_{kj}$，於是

$$P(X_1 = a_i | X_2 = b_j) = \frac {p_{ij}} {\sum_{k} p_{kj}} $$

$$P( X_2 = b_j | X_1 = a_i) = \frac {p_{ij}} {\sum_{k} p_{ik}} $$

貝葉斯決策理論

假設研究的分類有 c 個類別，各類別狀態用$w_i$表示，各類別出現的先驗概率為$P(w_i)$，特征空間的某一向量$\vec x = [x_1, x_2, ..., x_d]^T$，維度為 d，且條件概率密度 $p(\vec x|w_i)$是已知的（分類為$w_i$的樣本中，特征向量等於$\vec x$占比），於是利用貝葉斯公式得到後驗概率，

$$p(w_i | \vec x) = \frac {p(\vec x | w_i)p(w_i)} {\sum_{j=1}^c p(\vec x | w_j)p(w_j)}$$

如果$p(w_i| \vec x) = \max_{j=1,2,...,c} p(w_j|\vec x)$，那麽，$\vec x \in w_i$

因為後驗概率右端分母為$p(\vec x)$可以看作常數，所以

如果$p(\vec x|w_i)p(w_i) = \max_{j=1,2,...,c} p(\vec x| w_j)p(w_j)$，那麽，$\vec x \in w_i$

期望和方差

隨機變量X的概率分布為$P(X=x_k)= p_k$，若級數$\sum_{k} x_k p_k$絕對收斂，則X的數學期望或者概率平均值為

$$E(X)=\sum_{k} x_k p_k$$

方差為

$$var(X) = E((X-E(X))^2) = E(X^2) - E^2 (X) $$

標準差為$\sqrt {var(X)}$

熵

隨機變量X的概率分布為$p(x) = P(X=x)$，則熵（也稱自信息）定義為

$$H(X) = - \sum p(x)log_{2} p(x)$$

約定$0 log 0 = 0$

聯合熵和條件熵

聯合熵

$$H(X,Y) = - \sum{x \in X} \sum_{y \in Y} p(x,y) log p(x,y)$$

條件熵

\begin{aligned} H(Y|X) & = \sum_{x \in X} p(x) H(Y|X = x) \\ & = \sum_{x \in X} p(x) [- \sum_{y \in Y} p(y|x) log p(y|x)] \\ & = - \sum_{x \in X} \sum_{y \in Y} p(x,y) log p(y|x) \end{aligned}

將聯合熵公式中的$logp(x,y)$ 展開，得

\begin{aligned} H(X,Y) = - \sum{x \in X} \sum_{y \in Y} p(x,y) log p(x,y) \\ & = - \sum_{x \in X} \sum_{y \in Y} p(x,y) log[p(x)p(y|x)] \\ & = - \sum_{x \in X} \sum_{y \in Y} p(x,y) log p(x) - \sum_{x \in X} \sum_{y \in Y} p(x,y) logp(y|x) \\ & = -\sum_{x \in X} p(x)log p(x) + H(Y|X) \\ & = H(X) + H(Y|X) \end{aligned}

一般地，

$$H(X_1,X_2,...,X_n) = H(X_1) + H(X_2|X_1) + ... + H(X_n|X_1,X_2,...,X_{n-1})$$

互信息

根據熵的連鎖規則有

$$H(X,Y) = H(X) + H(Y|X) = H(Y) + H(X|Y) $$

於是，

$$H(X) - H(X|Y) = H(Y) - H(Y|X)$$

這個差就是X和Y的互信息，記作$I(X;Y)$，反應了知道Y值後X的不確定性的減少量，或者說Y的值透露了多少關於X的信息量，如下圖

\begin{aligned} I(X;Y) & = H(X) - H(X|Y) \\ & = H(X) + H(Y) - H(X,Y) \\ & = - \sum_{x}p(x)log p(x) - \sum_{y} p(y) log p(y) + \sum_{x,y} p(x,y) log p(x,y) \\ & = - \sum_{x,y} p(x,y) log p(x) - \sum_{x,y} p(x,y) log p(y) + \sum_{x,y} p(x,y) log p(x,y) \\ & = \sum_{x,y} p(x,y) log {\frac {p(x,y)} {p(x)p(y)}} \end{aligned}

由於$H(X|X) = 0$，所以

$$H(X) = H(X) - H(X|X) = I(X;X) $$

條件互信息

$$I(X;Y|Z)=H(X|Z) - H(X|Y,Z)$$

向量互信息

$$I(X_{1n};Y)=I(X_1;Y) + I(X_2;Y|X_1) + I(X_n;Y|X_1,X_2,...,X_{n-1}) = \sum_{i=1}^n I(X_i;Y|X_1,...,X_{i-1})$$

相對熵

兩個概率分布$p(x),q(x)$的相對熵定義為（這裏$p(x),q(x)$是兩個相同事件空間裏的概率分布，比如$p(x)$是真實概率分布，$q(x)$模型的概率分布即非真實分布，用來估計真實概率分布的），

$$D(p||q) = \sum_{x \in X} p(x) log {\frac {p(x)} {q(x)}} $$

約定$0 log(0/q) = 0$，$p log(p/0) = $

相對熵可以看作是$log{\frac {p(X)} {q(X)}}$的期望，

$$D(p||q) = E_{p}(log{\frac {p(X)} {q(X)}})$$

顯然，相對熵表示兩個概率分布的差距的測度，當$p=q$時，$D(p||q)=0$

互信息就是聯合分布與獨立性差距的測度，

$$I(X;Y)=D[p(x,y) || p(x)q(x)] $$

證明：

\begin{aligned} I(X;Y) & = H(X) - H(X|Y) \\ & = - \sum_{x \in X} p(x) log p(x) + \sum_{x \in X} \sum_{y \in Y} p(x,y) log p(x|y) \\ & = \sum_{x \in X} \sum_{y \in Y} p(x,y) log {\frac {p(x|y} {p(x)}} \\ & = \sum_{x \in X} \sum_{y \in Y} p(x,y) log {\frac {p(x,y)} {p(x)q(y)}} \\ & = D[p(x,y) || p(x)q(x)] \end{aligned}

條件相對熵根據定義不難得到，

$$D[p(y|x)||q(y|x)]=\sum_{x,y}p(x,y) log{\frac {p(y|x)} {q(y|x)}} = \sum_{x} p(x) \sum_{y} p(y|x) log{\frac {p(y|x)} {q(y|x)}}$$

聯合概率的相對熵為，

$$D[p(x,y) || q(x,y)] = D(p(x) || q(x)) + D[p(y|x) || q(y|x)]$$

證明：

\begin{aligned} D[p(x,y) || q(x,y)] & = \sum_{x,y} p(x,y) log { \frac {p(x,y)} {q(x,y)} } \\ & = \sum_{x,y} p(x,y) log { \frac {p(x) p(y|x)} {q(x) q(y|x)} } \\ & = \sum_{x,y} p(x,y) log { \frac {p(x)} {q(x)}} + \sum_{x,y} p(x,y) log { \frac {p(y|x)} {q(y|x)}} \\ & = \sum_{x} log{ \frac {p(x)} {q(x)}} \sum_{y} p(x,y) + D[p(y|x)||q(y|x)] \\ & = \sum_{x} log{ \frac {p(x)} {q(x)}} p(x) + D[p(y|x)||q(y|x)] \\ & = D(p(x) || q(x)) + D[p(y|x) || q(y|x)] \end{aligned}

交叉熵

根據熵的定義，我們知道熵的本質是香農信息量$log{\frac 1 {p(x)}}$的期望。

交叉這個詞意味什麽？想一想，然後我們給出交叉熵的定義，給出一個隨機變量$X ~ p(x)$，$q(x)$為近似$p(x)$的概率分布，則隨機變量X的真實分布p與模型（非真實分布）q之間的交叉熵為，

$$H(X,q) = H(p,q) = H(X) + D(p||q) = - \sum_{x} p(x) log q(x) = E_{p} (log{\frac 1 {q(x)}}) $$

可以看出交叉熵是$log{\frac 1 {q(x)}}$的期望，其中期望使用了真實概率分布$p(x)$，因為熵的計算用到了$p(x)$和$q(x)$，所以稱為交叉熵。

我們知道熵$H(p) = - \sum_{x} p(x) log p(x)$也可以用來表示平均編碼長度，則交叉熵$H(p,q)$就是使用非真實分布 q 來計算平均編碼長度，而$H(p,q) \ge H(p)$，當q 為真實分布 p 時等號成立。

證明：

我們使用拉格朗日乘子法來計算$H(p,q)$的極值，其中p是固定的，q是變量，當q = p 時，$H(p,q)$有極小值為$H(p)$，約束為$\sum_{x} q(x) = 1$，拉格朗日函數為，

$$L = - \sum_{x} p(x) logq(x) + \lambda (\sum_{x} q(x) - 1)$$

對$q(x)$求偏導並令其等於0，

$$\frac {\partial L} {\partial q(x)} = - \frac {p(x)} {q(x)} ln2 + \lambda = 0 $$

註意，隨便變量有多少個離散值x，就有多少個上式方程，變換一下，不難得到，

$$q(x) = p(x) \frac {\lambda} {ln 2}$$

對$\lambda$求偏導並令其等於0，

$$\sum_{x} q(x) - 1 = 0 $$

此即約束條件，於是

$$\sum_{x} q(x) = \frac {\lambda} {ln 2} \sum_{x} p(x) = \frac {\lambda} {ln 2} = 1$$

於是，

$$q(x) = p(x)$$

此時$H(p,q) = - \sum_{x} p(x) log q(x) = - \sum_{x} p(x) log p(x) = H(p) $

上式表明q=p時，H(p,q)取極值H(p)，下面再證明是極小值即可。

對H(p,q)求二階導得，

$$H(p,q)‘ = - \frac {p(x)} {q(x)} ln2$$

$$H(p,q)‘‘ = \frac {p(x)} {q^{2}(x)} ln2 $$

可見$H(p,q)‘‘ \ge 0$，即 $H(p,q)$是一個下凸函數，有極小值，於是$H(p,q) \ge H(p)$得證。

上一小節中講到的相對熵的概念也可以理解為使用非真實分布 q 得到的平均編碼長度比使用真實分布 p 得到的平均編碼長度多出的bit數：$D(p||q) = H(p,q) - H(p)$

語言模型

假設語言為L，語句是由單詞組成的序列，即$W_{i}^n = (w_1,w_2,...w_n)$表示由n個單詞組成的語句，那麽基於語句的熵為

$$H(w_1,w_2,...w_n) = - \sum_{W_{i}^n \in L} p(W_{i}^n) log p(W_{i}^n) $$

平均每個單詞的熵（entropy rate）為

$$\frac 1 n H(w_1,w_2,...w_n) = - \frac 1 n \sum_{W_{i}^n \in L} p(W_{i}^n) log p(W_{i}^n) $$

想要測量語言的真實熵，需要假設單詞序列的長度很大，假設語言是產生一系列單詞的隨機過程L，其平均每個單詞的熵（entropy rate）H(L)定義為，

$$H(L) = - \lim_{n \rightarrow \infty} \frac 1 n H(w_1,w_2,...w_n) = - \lim_{n \rightarrow \infty} \frac 1 n p(w_1,w_2,...w_n) log p(w_1,w_2,...w_n) $$

假設語言L 是穩態遍歷的隨機過程，根據Shannon-McMillan-Breiman理論有，

$$\frac 1 n H(w_1,w_2,...w_n) = \lim_{n \rightarrow \infty} - \frac 1 n log p(w_1,w_2,...w_n) $$

定義語言L其模型q的交叉熵為

$$H(L,q) = - \lim_{n \rightarrow \infty} \frac 1 n \sum_{W} p(w_1,w_2,...w_n) log q(w_1,w_2,...w_n) $$

其中，$p(w_1,w_2,...w_n)$表示語句出現的真實概率，$q(w_1,w_2,...w_n)$表示 模型q 對語句的概率估計。

再次根據Shannon-McMillan-Breiman理論，假設語言L 是穩態遍歷的隨機過程，則

$$H(L,q) = - \lim_{n \rightarrow \infty} \frac 1 n log q(w_1,w_2,...w_n)$$

困惑度

設計語言模型時，通常用困惑度（perplexity）來代替交叉熵衡量語言模型的好壞。語言L中的單詞序列$(w_1,w_2,...w_n)$，則語言的困惑度為

$$PP_{q} = 2^{H(L, q)} = 2^{- \lim_{n \rightarrow \infty} \frac 1 n log q(w_1,w_2,...w_n)} \approx q(w_1,w_2,...w_n)^{- \frac 1 n} $$

噪聲信道模型

信息熵可以定量的估計信源每發送一個符號所提供的平均信息量。信號傳輸過程需要進行雙重處理：1. 對編碼進行壓縮，盡量消除冗余。2. 由於信道有噪聲，信道輸出並不等於輸入而是有一定信息的錯誤，所以需要通過增加一定的可控冗余以保障輸入經過噪聲信道後可以很好的恢復原樣，這個可控冗余能檢測和校驗傳輸造成的錯誤。過程如下圖

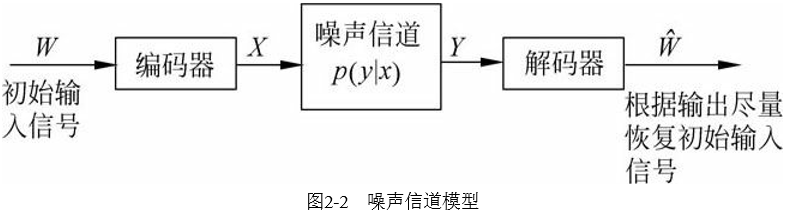
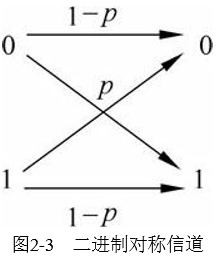
一個二進制對稱信道的輸入符號集為$X = \lbrace 0, \quad 1 \rbrace$，輸出符號集為$X = \lbrace 0, \quad 1 \rbrace$。傳輸過程中如果符號被誤傳的概率為p，則正確傳輸的概率為 1- p，如下圖

假設輸入為X，輸出為Y，如果Y很很好的逼近X，則信道的保真能力就很強，根據前面對互信息的介紹，我們定義信道容量為，

$$C = \max_{p(X)} I(X;Y)$$

輸入和輸出的互信息達到最大值，這就是信道的最大傳輸容量

在自然語言處理中不需要編碼，自然語言的句子可視為已編碼的符號序列，但是需要解碼，使觀察到的輸入序列更接近與輸入，如下圖，輸入為I，經過信道輸出為可觀測序列O，解碼得到原始輸入$\hat I$.

從所有可能的 I 中求解使得 p(O|I) 最大的那個I 認為是輸入 $\hat I$，根據貝葉斯公式，已知可觀察的輸出O的條件下，p(O)已經確定為一定值，

$$\hat I = arg \max_{I} p(I|O) = arg \max_{I} \frac {p(I)p(O|I)} {p(O)} = arg \max_{I} p(I)p(O|I)$$

上式中，p(I)是語言模型，是指語言中 單詞序列$(w_1,w_2,...w_n)$ 的概率分布，而 p(O|I)稱為信道概率。例如，將一個法語句子 f 翻譯成英語 e，那麽翻譯信道模型就是假設法語句子是觀測到的輸出 O，它原本的輸入I 是一個英語句子 e，但通過噪聲信號變成了法語句子 f，現在需要根據概率 p(e) 和 p(f|e) 計算求出最接近原始輸入英語句子e 的解 $\hat e$。

統計學習基本理論知識（一）