數論

筆記：Neworld2002

什麽是數論

• 研究整數的純數學分支，整數的基本元素是素數，所以數論的本質是對素數性質的研究。

素數

基本概念

• 整數集合\(Z\){-1,0,1...}

• 自然數集合\(N\){0,1,2,...}

• 整除 ：若\(a=bk\)，三數均為整數，則\(b\)整除\(a\)

• 約數：若\(b\)整除\(a\)，且\(b\geqslant0\)，則b是a的約數

  • 1整除任何數，任何數整除0

  • 若a整除b，a整除c，則a整除(b+c)，a整數(b-c)

    • 證明：

    • \(\because a\)整除\(b\)，\(a\)整除\(c\)，\((a \neq 0)\)

      \(\therefore b = an ,c = am\)

      \(\therefore (b+c) = an+am = a(n+m)\)

      \(\therefore a\)整除\((b+c)\)

      同理可證，\(a\)整除\((b-c)\)

  • 若a整除b，則對任何數c，都有a整除(bc)

  • 若a整除b，b整除c，則a整除c

    • 證明：

    • \(\because a\)整除b，\(b\)整除\(c\)

      \(\therefore an = b , bm = c\)

      \(\therefore anm = c\)

      \(\therefore a\)整除\(c\)

    • 即傳遞性

• 因子：對一個正整數a來說，除了1和a本身，其他約數均為它的因子

素數與合數

• 素數：所有大於1且只被自己和1整除的數
• 合數：所有大於1且不是素數的數
• 其他整數(0,1,負整數)既不是素數，也不是合數
• 素數有無窮多個，但分布較為稀疏，不大於N的素數約有\(\frac{N}{ln(N)}\)

素數判定

• 若N是一個合數，則N至少有一個素因子（是素數且是N的因子的數），因此最小的素因子一定不大於\(\sqrt{N}\)

樸素判斷

• 已知：最小的素因子一定不大於\(\sqrt{N}\)
• 所以我們只需要枚舉[2,\(\sqrt{N}\)]之間的數，若存在一個數x，使得x整除N，就代表N存在一個因子，N就不是素數

//c++
inline bool Prime(int n){
    if(n==1)return false;
    for(register int i=2;i*i<=n;++i){
        if(n%i==0)return false;
    }
    return true;
}
 

// pascal
function prime(n:longint):boolean;
var i:longint;
begin
    if(n==1)exit(false);
    for i:=2 to trunc(sqrt(n)) do
        if(n mod i = 0)exit(false)；
    exit(true);
end;

整數惟一分解定律

• 若整數\(N \geqslant 2\)，那麽\(N\)一定可以惟一地表示為若幹素數的乘積（素因子）。

• \[ N = p_1^{r_1} p_2^{r_2}... p_k^{r_k} (p_i為素數，r_i\geqslant 0) \]

  18 = 2 * 3 * 3 = 2^1 * 3^2

  45 = 3 * 3 * 5

  .....

  顯而易見，對於一個合數N，一定存在兩個數，使其相乘為N，這兩個數就是N的因子。

  若這兩個數不為素數，則可以繼續將這兩個數分解，直至得到素數。

  綜上所述，一個合數N，是由多個素因子相乘得到。

  設\(N = am\)，\(a\)和\(m\)都是N的因子，且\(a\)為N的素因子，\(a\)是N最小的素因子

素數分解

• \\c++
  std::vector<int> fac(int x){
      vector<int>ret;
      for(register int i=2;i*i<=x;++i){//循環每個質因數
        while(x%i==0){//如果i整除x
            ret.push_back(i);//把i放進數組裏
               x /= i;//除去掉一個i
          }
      }
      if(x>1)ret.push_back(x);
      return ret;
  }

• \\pascal 不會寫

• 代碼思路

• 不想寫pascal……

  考慮開一個數組，從小到大枚舉x的素因數，然後判斷這個數是否整除x，如果整除就把它丟進數組裏，並且x div 它，去掉這個數。由於這個數可能出現多次：如4 = 2*2，所以要弄個while循環除以它，直到x不含有這個數

素數篩法

Eratosthenes篩

• 這個名字讀法很多。直接稱為埃式篩法
• 每個合數a一定可以寫成a=px的形式，其中p是素數，x是倍數(\(x\neq1\))
• 對於[1,n]內的素數p，枚舉倍數x，把px標記為合數，剩下的是素數，這就是埃式篩法
• 改進：對於素數p，只篩倍數x\(\geqslant\)p的數，如果x\(<\)p，則x中一定有比p小的素因子，px會在之前被篩出。
• 因此只需要考慮[2,\(\sqrt{N}\)]範圍內素數
• 時間復雜度\(O(nloglogn)\)

代碼思路

• 開一個數組，可以是整型也可以是布爾型。1（true）表示是素數，0（false）表示合數。
• 對於一個數x，數組prime[x]若為1（true），則是素數，否則反之。
• 初始化所有值為1（true）
• 然後把prime[0]和prime[1]標為0（false）
• 從2到\(\sqrt{N}\)開始循環
• 如果此時prime[i]為1（true），則i一定為素數，如果是合數，在此之前一定被篩過
• 然後以i為p，循環x，若px超過N就終止循環，在過程中把prime[px]標記為0或false

#define MAXN 200005
bool prime[MAXN];
void eratos(int N){
    std::memset(prime,true,sizeof(prime));
    prime[0] = prime[1] = false;
    for(register int i=2;i*i<=N;++i)
        if(prime[i]==true){
            for(register int j=i*i;j<=N;j+=i)prime[j]=false;
        }
}

篩法優化素因數分解

• 利用埃式篩法可以快速實現素因數分解
• 首先定義數組：Minfac[x]記錄x的最小素因子，prime[x]表示x是否為素數
• 初始化所有Minfac[x] = x，表示還沒有找到素因子，prime[x]為true

#define MAXN 1000000
bool prime[MAXN];
int Minfac[MAXN];
void init(int n){//初始化
    prime[0] = prime[1] = false;//0和1都不是素數
    Minfac[0] = Minfac[1] = -1//兩數都沒有素因子
        for(register int i=2;i<=n;++i){
            prime[i] = true;
            Minfac[i] = i;
        }
}

• 然後直接開始篩法，篩的過程中記錄Minfac即可

void eratos(int n){
    for(register int i=2;i*i<=n;++i){
        if(prime[i]==true){//如果是質數
            for(register int j=i*i;j<=n;j+=i){
                prime[j] = false;//將其倍速設為false
                if(Minfac[j]==j){//如果之前沒有找打這個數的最小素因子
                    Minfac[j] = i;//i就是它的最小素因子
                }
            }
        }
    }
}

• 然後我們就可以開始分解了。由於之前我們已經提前將所有數的最小素因子算出，就省去了一個個找素因子的時間。

std::vector<int> factor(int x){
    std::vector<int>res;
    while(x>1){
        ret.push_back(Minfac[x]);//將最小的素因子加入數組
        x /= Minfac[x];//除掉它
    }
}

歐拉篩(線性篩)

• 顯而易見埃式篩法會出現一個數被篩多次。

  30 = 2·15 = 3·10 = 5·6

• 30這個數就被2、3、5篩了三次

• 如果每個合數只被它的最小素因子篩出，那麽這個數只被篩一次

• 時間復雜度可以達到\(O(N)\)，是線性的

代碼思路

• 枚舉[2,n]中的每個數i
• 如果i是素數保存到素數表內
• 利用i和之前素數表中的素數prime[j]去篩i·prime[j]，為確保i·prime[j]只被prime[j]篩過一次，要確保prime[j]是i·prime[j]的最小素因子，即i中不能有比prime[j]還要小的素因子

void Euler_sieve(int n){
    std::memset(isprime,true,sizeof(isprime));//初始化所有數都是素數
    int tot = 0;//tot記錄素數數量
    for(register int i=2;i<=n;++i){
        if(isprime[i]){//如果這個數是素數
            tot += 1;//素數數量+1
            prime[tot] = i;//放入素數表內
        }
        for(register int j=1;j<=tot;++j){//遍歷素數表
            if(i*prime[j]>n)break;//超過n就沒必要繼續篩了
            isprime[i*prime[j]] = false;//把i*prime[j]篩掉
            if(i%prime[j]==0)break;
            //當i中含有prime[j]這個素因子時應該停止循環，避免之後出現比prime[j]更大的素因子，使得每個數只被最小素因子篩掉
        }
    }
    
}

約數

整數惟一分解定理的推論

• 若\(N \geqslant 2\)，那麽\(N = p_1^{r_1}p_2^{r_2}...p_k^{r_k}(p_i為素數,r_i\geq 0)\)
• \(N\)的正約數集合為:{\(p_1^{b_1}p_2^{b_2}...p_k^{b_k}(0 \leqslant b_i \leqslant r_i)\)}
• \(N\)的正約數個數為：\((r_1+1)(r_2+1)...(r_k+1) = \prod_{i=1}^{k}(r_i+1)\)

舉例：

12的正約數有6個：1、2、3、4、6、12

將12分解素因數得：\(12 = 2^2 · 3^1\)

\((r_1+1)(r_2+1) = (2+1)(1+1) = 6\)

證明如下：

首先同上，n可以分解質因數：\(N = p_1^{r_1}p_2^{r_2}...p_k^{r_k}(p_i為素數,r_i\geq 0)\)

由約數定義可知\(p_1^{r_1}\)的約數有:\(p_1^0 、p_2^1、p_1^3 ... p_1^{r_1}\) ，共(\(r_1+1\))個;同理\(P_2^{r_2}\)的約數有(\(r_2+1\))個......\(p_k^{r_k}\)的約數有(\(r_k+1\))個。

故根據乘法原理：n的約數的個數就是\((r_1+1)(r_2+1)...(r_k+1) = \prod_{i=1}^{k}(r_i+1)\)

——《百度百科》約數個數定理

• 除了完全平方數，約數總是成對出現的，即\(d\leqslant \sqrt{N}\)和\(\frac{N}{d} \leqslant \sqrt{N}\)都是\(N\)的約數

• \(N\)的約數個數上界為\(2\sqrt{N}\)

• \(N\)所有的正約數和為：\((1+p_1+p_1^{2}+...+p_1^{r_1})(1+p_2+p_2^{2}+...+p_2^{r_2})...(1+p_k+p_k^{2}+...+p_k^{r_k}) = \prod_{i=1}^{k}(\sum_{j=0}^{r_i}p_i^j)\)

最大公約數

定義

設\(a\)和\(b\)都是不為0的整數，\(c\)為滿足整除\(a\)也整除\(b\)的最大整數，則稱\(c\)為\(a\)、\(b\)的最大公約數，記為\(gcd(a,b)\)

性質

• \(gcd(a,b) = gcd(b,a)\)
• \(gcd(a,0) = a\)
• \(gcd(a,b) = gcd(-a,b)\)
• \(gcd(a,ka) = a\)
• \(gcd(a,b) = gcd(|a|,|b|)\)
• \(gcd(an,bn) = n · gcd(a,b)\)
• 若\(d\)整除\(a和b\)，則\(d\)整除\(gcd(a,b)\)
• \(gcd(a,b) = gcd(a,ka+b)\)

計算gcd

枚舉法

從\(min(a,b)\)到1枚舉\(i\)，判斷是否能整除兩數，如果可以就輸出並退出循環

時間復雜度\(O(min(a,b))\)

min(a,b) = a和b的較小值

max(a,b) = a和b的較大值

分解素因數

當\(a = p_1^{r_2}p_2^{r_2}..p_k^{r_k} , b = p_1^{s_1}p_2^{s_2}..p_k^{s_k}\)時，第\(i\)項的\(r_i , s_i \geqslant 0\)

則\(gcd(a,b) = p_1^{min(r_1,s_1)}p_2^{min(r_2,s_2)}...p_k^{min(r_k,s_k)}\)

代碼思路

• 設答案為\(ans\)，並初始化為1
• 枚舉[2,\(\sqrt{min(a,b)}\)]之間的數\(i\)
• 當兩數均同時能被\(i\)整除，則一直除以\(i\)，並\(ans\)一直乘以\(i\)，直至兩數出現一數不能整除\(i\)
• 如果兩數其中之一還有\(i\)的倍數，則此數繼續除以\(i\)，直至此數不含有\(i\)這個因子為止
• 循環上述步驟
• 循環結束後，需要進行特判：若\(a\)整除\(b\)，\(ans\)應乘以\(a\)
• 若\(b\)整除\(a\)，則\(ans\)乘以\(b\)
• 最後\(gcd(a,b) = ans\)

int gcd(int a,int b){
    int ans = 1;
    for(register int i=2;i*i<=std::min(a,b);++i){
        while(a%i==0&&b%i==0){//當兩數均含i這個因子
            a/=i;b/=i;ans*=i;//除去這個質因子，並且ans乘上i
        }
        while(a%i==0)a/=x;//若a還含有i這個因子，應該去幹凈
        while(b%i==0)b/=x;//同上
    }
    if(a%b==0)ans*=b;//如果b整除a
    else if(b%a==0)ans*=a;//如果a整除b
    return ans;//ans即為答案
}

時間復雜度約為\(O(\sqrt{min(a,b)})\)

自己估計的好像不準

以上兩個算法時間慢，還不好寫，直接丟棄。

歐幾裏得算法

先上代碼

int gcd(int a,intb){
    if(b==0)return a;
    else return gcd(b,a%b);
}

沒錯，寫完了。

當然在C++裏還可以寫得更短

int gcd(int a,int b){return b==0 ? a : gcd(b,a%b);}

時間復雜度為\(O(log(a+b))\)，不管在效率還是代碼量方面都碾壓上述算法

算法說明

該算法也叫輾轉相除法

根據上面的代碼，我們會發現是基於\(gcd(a,b) = gcd(b,a\bmod b)\)

求證：\(gcd(a,b) = gcd(b,a\bmod b)\)

證明如下：

設\(d\)為\(a\)和\(b\)的任意公約數，則有\(a = ld,b = md\)

\(\because a\geqslant b\)

\(\therefore b\)可以通過一次乘法和一次加法後得到\(a\)

\(\therefore a = bq+r (a \geqslant b)\)

將\(a = ld,b = md\)代入

得\(ld = mdq + r\)

移項得\(r = ld - mdq = d(l-mq)\)

則\(d\)為\(r\)的約數

\(\because a = bq+r\)

\(\therefore a \bmod b = r\)

又\(d\)為\(a,b\)的任意公約數

綜上所述，得：\(a,b\)的任意公約數，也都是\(a \bmod b\)的約數

\(\therefore gcd(a,b) = gcd(b,a \bmod b)\)

算法變換

[SDOI2009]SuperGCD

這道題直接用GCD是不行的，顯而易見是道高精題，但不過高精模可能比較尷尬，我不會寫

所以需要引入一些改進——適用於高精度數的二進制法

1. \(a<b\)時，\(gcd(a,b) = gcd(b,a)\)

2. \(a = b\)時，\(gcd(a,b) = a\)

3. \(a,b\)均為偶數時，\(gcd(a,b) = 2*gcd(a/2,b/2)\)

4. \(a\)為偶數\(b\)為奇數時，則\(b\)中必無2這個因子，所以\(gcd(a,b) = gcd(a/2,b)\)

5. \(b\)為偶數\(a\)為奇數時，則\(a\)中必無2這個因子，所以\(gcd(a,b) = gcd(a,b/2)\)

6. 若兩數都是奇數，\(gcd(a,b) = gcd(b,a-b)\)，這步也叫更相減損術，出自《九章算術》

代碼實現時切記傳參傳數組。

最小公倍數

• \(a,b\)的最小公倍數記作\(lcm(a,b)\)

性質

• \(lcm(a,b) = \frac{ab}{gcd(a,b)}\)，這也是求\(lcm\)的常用方法
• 若\(a,b\)整除\(m\)，則\(lcm(a,b)\)整除\(m\)
• 若\(a,b,m\)是正整數，則\(lcm(ma,mb) = m · lcm(a,b)\)

容斥原理

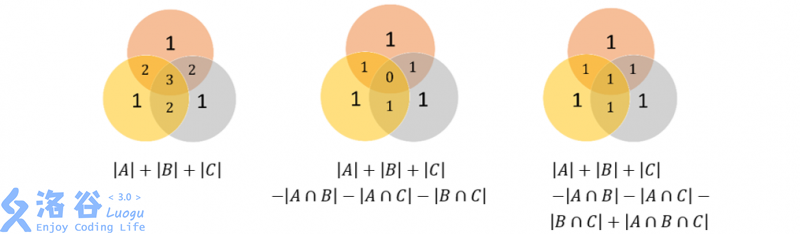
• 現在有$S = ${\(1,2,3,...,600\)}，求其中可被2，3，5整除的數的數目
• 令\(A,B,C\)分別為能被2，3，5整除的數的集合，可得：

\[ |A| = \lfloor \frac{600}{2} \rfloor = 300, |B| = \lfloor \frac{600}{3} \rfloor = 200,|C| = \lfloor \frac{600}{5} \rfloor = 120 \]

• \(\lfloor \frac{a}{b}\rfloor\)是a/b向下取整的意思
• 顯然\(A,B,C\)中會含有相同的元素，可繼續求\(A,B,C\)的交集，可得

\[ |A \cap B| = \lfloor \frac{600}{2*3}\rfloor = 100,|A \cap C| = \lfloor \frac{600}{2*5}\rfloor = 60,|B \cap C| = \lfloor \frac{600}{3*5}\rfloor = 40 \]

• 最後求\(A,B,C\)的三個集合的交集情況

\[ |A \cap B \cap C| = \lfloor \frac{600}{2*3*5}\rfloor = 20 \]

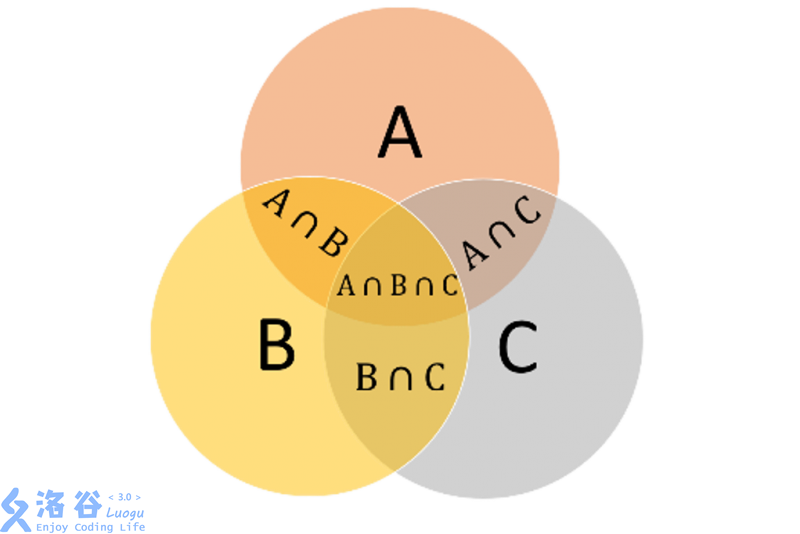
定義

• 具有性質A或者具有性質B的元素個數，等於具有性質A的元素個數與具有性質B的元素個數的和，減去同時具有性質A和性質B的元素個數。使得計算無遺漏無重復，這就是容斥原理。

歐拉函數

定義

• 互素：若\(gcd(a,b)=1\)，則稱\(a,b\)互素（互質），記作\(a \perp b\)
• 歐拉函數\(\varphi(n)\)：（讀作fai），定義為[1,n)中與n互素的數的個數

\(\varphi(8) = 4\)

小於8且與8互素的數是1，3，5，7

• 推論：若\(p\)為素數，則\(\varphi(p) = p-1\)

求歐拉函數

容斥原理求歐拉函數

• 若將\(N\)分解為不同素數的乘積，即：

• \(N = p_1^{r_1}p_2^{r_2}...p_k^{r_k}\)

• 設1到\(N\)中的數，為\(p_i\)的倍數的集合為\(A_i\)，$|A_i| = \lfloor \frac{N}{p_i}\rfloor(i=1,2,..,k) $

• 對於$p_i \neq p_j,A_i \cap A_j \(即是\)p_i\(和\)p_j$的公倍數，即

• \(|A_i \cap A_j| = \lfloor \frac{N}{p_ip_j}\rfloor(1 \leq i,j \leq k,i \neq j)\)

• 在取出\(|A_i||A_j|\)時，\(p_i,p_j\)的公倍數被去除了兩次，所以要加回來
  \[ \varphi(N) = N - (\frac{N}{p_1}+\frac{N}{p_2}+...+\frac{N}{p_k}) + (\frac{N}{p_1p_2}+\frac{N}{p_2p_3}+...+\frac{N}{p_1p_k}) \pm (\frac{N}{p_1p_2..p_k}) \]

  \[ \varphi(N) = N(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_k}) \]

int euler_phi(int n){
    int res = n;
    for(register int i=2;i*i<=n;++i){
        if(n%i==0){
            res = res / i * (i-1);
            for(;n%i==0;n/=i);
        }
    }
    if(n!=1)res = res / n * (n-1);
    return res;
}

時間復雜度為\(O(\sqrt{N})\)

埃式篩法求歐拉函數

int euler[MAXN];
void euler_phi(){
    for(register int i=0;i<MAXN;++i)euler[i] = i;
    for(register int i=2;i<MAXN;++i){
        if(euler[i]==i){
            for(register int j=i;j<MAXN;j+=i)
                euler[j] = euler[j] / i * (i-1);
        }
    }
}

篩出一個歐拉函數表

性質

• 若\(a,b\)互素，則\(\varphi(ab) = \varphi(a)\varphi(b)\)

同余

基本概念

• 除法定理：\(a = qm+r\)，其中\(q = \lfloor\frac{a}{m}\rfloor\)為商，\(r = a \bmod m\)為余數
• 同余：如果$a \bmod p = b \bmod p \(，則\)a,b\(除以\)m\(的余數相等，記作：\)a \equiv b \pmod m$
• 若\(a \equiv b \pmod m\)，則\(gcd(a,m) = gcd(b,m)\)

證明：

\(\because gcd(a,m) = gcd(m,a\bmod m),gcd(b,m) = gcd(m,b\bmod m)\)

又\(a \bmod m = b \bmod m\)

\(\therefore gcd(a,m) = gcd(b,m)(a \equiv b \pmod m)\)

• 若\(a \equiv b \pmod m\)，且\(d\)整除\(m\)，則\(a \equiv b \pmod d\)

剩余系

• 指模正整數\(N\)的余數所組成的集合
• 如果一個剩余系包括了這個正整數\(N\)所有可能的余數(0,1,2,...N-1) ，則稱為完全剩余系，記作\(Z_N\)
• 簡化剩余系：完全剩余系中與\(N\)互素的數的集合，記作\(Z_N^*\)

模運算

• 如果\(a \equiv b\pmod m ,c\equiv d \pmod m\)，則有
  • \(a + c \equiv b +d \pmod m\)
  • \(a- c \equiv b-d \pmod m\)
  • $ac \equiv bd\pmod m $
• \((a+b)\bmod m = ((a\bmod m)+(b\bmod m))\bmod m\)
• $(a-b)\bmod m = ((a)\bmod m - (b)\bmod m + m)\bmod m $
• \((a*b)\bmod m = ((a\bmod m)*(b\bmod m))\bmod m\)

費馬小定理

#### 定義

• 若\(p\)為素數，且\(a,p\)互素，則有 \(a^{p-1} \equiv 1 \pmod p\)

證明

• \(p-1\)個整數，\(a,2a,3a,...,(p-1)a\)中沒有一個是\(p\)的倍數，而且沒有任意兩個模\(p\)同余。
• 所以這\(p-1\)個數對模\(p\)的同余是\(1,2,3,...,(p-1)\)的一個排列
• 可得：$a2a3a..(p-1)a\equiv 123...(p-1)\pmod p $
• 化簡得\(a^{p-1}*(p-1)! \equiv (p-1)! \pmod p\)
• 得：\(a^{p-1} \equiv 1 \pmod p\)

歐拉定理

• 若\(a,m\)互素，則有\(a^{\varphi(m)} \equiv 1 \pmod m\)
• 可看作費馬小定理的加強，當模數不為素數時應使用歐拉定理

歐拉定理的推論

• 若\(a,m\)互素，則有\(a^b \equiv a^{b \bmod \varphi(m) } \pmod m\)
• 證明：

設\(b = q*\varphi(m) + r\)，其中\(0 \leq r \leq \varphi(m)\)，即\(r = b \bmod \varphi(m)\)

則$a^b \equiv a^{q\varphi(m)+r} \equiv (a^{\varphi(m)})^qa^r \equiv 1^q*a^r \equiv a^r \equiv a^{b \bmod \varphi(m)}\pmod m $

逆元

定義

已知整數a與整數p互質，即gcd(a,p)=1，定義關於x的方程，稱x為a關於模p的逆元
\[ ax \equiv 1 \pmod p \]
我們需要特別註意，當兩數不是互質時，沒有逆元

逆元的作用

通常情況下，有些題目會要求我們MOD一個數，我們可以通過同余定理來計算

但是需要特別註意，如下式
\[ (a/b) \bmod p \]
不可以寫成
\[ (a \bmod p) / (b \bmod p)\bmod p \]
但可以寫成其中b^-1是a關於模p的逆元

求解逆元

費馬小定理

假如a是整數，p是質數，則a,p顯然互質(即兩者只有一個公約數，那麽我們可以得到費馬小定理的一個特例，即當p為質數時候， a^(p-1)≡1(mod p)

如上，我們需要特別註意，只能當p為質數時，才能使用費馬小定理求解逆元
\[ a^{p-1}\equiv 1 \pmod p \]

\[ a*a^{p-2}\equiv1 \pmod p \]

則可知，a^(p-2)為a關於模p的逆元，此時只需要快速冪求解即可

費馬小定理求逆元的時間復雜度是O(logN)，但常數較大

線性篩

#include <cstdio>
#define MAXN 3000005
long long N,P;
long long inv[MAXN];
int main(){

    scanf("%lld%lld",&N,&P);
    inv[1] = 1;
    puts("1");
    for(register int i=2;i<=N;++i){
        inv[i] = (P-(P/i))*(inv[P%i])%P;
        printf("%lld\n",inv[i]);
    }
    return 0;
}

拓展歐幾裏得算法

• \(ax+bx = gcd(a,b)\)
• 設\(a>b\)

1. 當\(b = 0\)時，\(gcd(a,b) = a\)。則\(x = 1,y = 0\)

2. 當\(ab \neq 0\)時，設\(ax_1 +by_1 = gcd(a,b),bx_2 + (a \bmod b)y_2 =gcd(b,a\bmod b)\)

   根據樸素的歐幾裏得原理有\(gcd(a,b) = gcd(b,a\bmod b)\)

   則：\(ax_1 + by_1 = bx_2 + (a \bmod b)y_2\)

   即：\(ax_1 +by_1 = bx_2 + (a -(a/b)*b)y_2 = bx_2 + ay_2 - (a/b)*by_2 = ay_2 - b((a/b)y_2-x_2)\)

   得：\(x_1 = y_2,y_1 = x_2 - (a/b)y_2\)

int x,y;
int exgcd(int a,int b,int &x,int &y){
    if(b==0){x=1;y=0;return a};
    int d = exgcd(b,a%b,y,x);
    y = y -a/b*x;
    return d;
}

拓展歐幾裏得算法的應用

• 求解不定方程

  • 對於整數方程\(ax+by= m\)，若\(m |gcd(a,b)\)，則方程存在整數解，否則不存在

• 求解線性方程（同余方程）與逆元

  • 若\(ax \equiv 1 \pmod p\)，且\(gcd(a,p)=1\)

    則有：\(ax + py = 1\)，且\(x\)為\(a\)的逆元

最後

• 筆記來源：2018FOI算法夏令營《數論及其應用》，各dalao博客

數論筆記1