線性代數

一、基本知識

本文中所有的向量都是列向量的形式： \[\mathbf{\vec x}=(x_1,x_2,\cdots,x_n)^T=\begin{bmatrix}x_1\\x_2\\ \vdots \\x_n\end{bmatrix}\] 本書中所有的矩 $\mathbf X\in \mathbb R^{m\times n}$ 都表示為： \[\mathbf X = \begin{bmatrix} x_{1,1}&x_{1,2}&\cdots&x_{1,n}\\ x_{2,1}&x_{2,2}&\cdots&x_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ x_{m,1}&x_{m,2}&\cdots&x_{m,n}\\ \end{bmatrix}\]

簡寫為 $(x_{i,j})_{m\times n}$ 或 $[x_{i,j}]_{m\times n}$ 。
矩陣的F範數：設矩 $\mathbf A=(a_{i,j})_{m\times n}$ ，則其F範數為 $||\mathbf A||_F=\sqrt{\sum_{i,j}a_{i,j}^{2}}$ 。它是向量 $L_2$ 範數的推廣。
矩陣的跡：設矩 $\mathbf A=(a_{i,j})_{m\times n}$ ， $ \mathbf A$ 的跡為 $tr(\mathbf A)=\sum_{i}a_{i,i}$ 。跡的性質有：
- $\mathbf A$
  
  的F 範數等 $\mathbf A\mathbf A^T$ 的跡的平方根 $||\mathbf A||_F=\sqrt{tr(\mathbf A \mathbf A^{T})}$ 。
- $\mathbf A$ 的跡等 $\mathbf A^T$ 的跡 $tr(\mathbf A)=tr(\mathbf A^{T})$ 。
- 交換律：假設 $\mathbf A\in \mathbb R^{m\times n},\mathbf B\in \mathbb R^{n\times m}$ ，則有 $tr(\mathbf A\mathbf B)=tr(\mathbf B\mathbf A)$
  
  。
- 結合律 $tr(\mathbf A\mathbf B\mathbf C)=tr(\mathbf C\mathbf A\mathbf B)=tr(\mathbf B\mathbf C\mathbf A)$ 。

二、向量操作

一組向 $\mathbf{\vec v}_1,\mathbf{\vec v}_2,\cdots,\mathbf{\vec v}_n$ 是線性相關的：指存在一組不全為零的實 $a_1,a_2,\cdots,a_n$ ，使得 $\sum_{i=1}^{n}a_i\mathbf{\vec v}_i=\mathbf{\vec 0}$ 。一組向 $\mathbf{\vec v}_1,\mathbf{\vec v}_2,\cdots,\mathbf{\vec v}_n$ 是線性無關的，當且僅 $a_i=0,i=1,2,\cdots,n$ 時，才有 $\sum_{i=1}^{n}a_i\mathbf{\vec v}_i=\mathbf{\vec 0}$ 。
一個向量空間所包含的最大線性無關向量的數目，稱作該向量空間的維數。
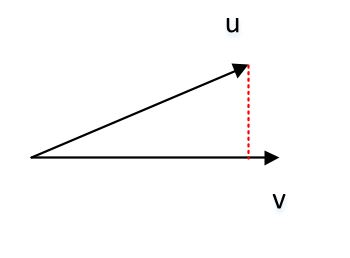
三維向量的點積 $\mathbf{\vec u}\cdot\mathbf{\vec v} =u _xv_x+u_yv_y+u_zv_z = |\mathbf{\vec u}| | \mathbf{\vec v}| \cos(\mathbf{\vec u},\mathbf{\vec v})$ 。
三維向量的叉積： \[\mathbf{\vec w}=\mathbf{\vec u}\times \mathbf{\vec v}=\begin{bmatrix}\mathbf{\vec i}& \mathbf{\vec j}&\mathbf{\vec k}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \end{bmatrix}\] 其 $\mathbf{\vec i}, \mathbf{\vec j},\mathbf{\vec k}$ 分別 $x,y,z$ 軸的單位向量。 \[\mathbf{\vec u}=u_x\mathbf{\vec i}+u_y\mathbf{\vec j}+u_z\mathbf{\vec k},\quad \mathbf{\vec v}=v_x\mathbf{\vec i}+v_y\mathbf{\vec j}+v_z\mathbf{\vec k}\]
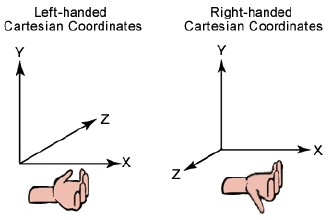
- $\mathbf{\vec u} $ 和 $\mathbf{\vec v}$ 的叉積垂直於 $\mathbf{\vec u},\mathbf{\vec v}$ 構成的平面，其方向符合右手規則。
- 叉積的模等於 $\mathbf{\vec u},\mathbf{\vec v}$ 構成的平行四邊形的面積
- $\mathbf{\vec u}\times \mathbf{\vec v}=-\mathbf{\vec v}\times \mathbf{\vec u}$
- $\mathbf{\vec u}\times( \mathbf{\vec v} \times \mathbf{\vec w})=(\mathbf{\vec u}\cdot \mathbf{\vec w})\mathbf{\vec v}-(\mathbf{\vec u}\cdot \mathbf{\vec v})\mathbf{\vec w} $
三維向量的混合積： \[[\mathbf{\vec u} \;\mathbf{\vec v} \;\mathbf{\vec w}]=(\mathbf{\vec u}\times \mathbf{\vec v})\cdot \mathbf{\vec w}= \mathbf{\vec u}\cdot (\mathbf{\vec v} \times \mathbf{\vec w})\\ =\begin{vmatrix} u_x&u_y&u_z\\ v_x&v_y&v_z\\ w_x&w_y&w_z \end{vmatrix} =\begin{vmatrix} u_x&v_x&w_x\\ u_y&v_y&w_y\\ u_z&v_z&w_z\end{vmatrix} \] 其物理意義為： $\mathbf{\vec u} ,\mathbf{\vec v} ,\mathbf{\vec w}$ 為三個稜邊所圍成的平行六面體的體積。 $\mathbf{\vec u} ,\mathbf{\vec v} ,\mathbf{\vec w}$ 構成右手系時，該平行六面體的體積為正號。
兩個向量的並矢：給定兩個向 $\mathbf {\vec x}=(x_1,x_2,\cdots,x_n)^{T}, \mathbf {\vec y}= (y_1,y_2,\cdots,y_m)^{T}$ ，則向量的並矢記作： \[\mathbf {\vec x}\mathbf {\vec y} =\begin{bmatrix}x_1y_1&x_1y_2&\cdots&x_1y_m\\ x_2y_1&x_2y_2&\cdots&x_2y_m\\ \vdots&\vdots&\ddots&\vdots\\ x_ny_1&x_ny_2&\cdots&x_ny_m\\ \end{bmatrix}\] 也記 $\mathbf {\vec x}\otimes\mathbf {\vec y}$ 或 $\mathbf {\vec x} \mathbf {\vec y}^{T}$ 。

三、矩陣運算

給定兩個矩 $\mathbf A=(a_{i,j}) \in \mathbb R^{m\times n},\mathbf B=(b_{i,j}) \in \mathbb R^{m\times n}$ ，定義：
- 阿達馬積Hadamard product（又稱作逐元素積）： \[\mathbf A \circ \mathbf B =\begin{bmatrix} a_{1,1}b_{1,1}&a_{1,2}b_{1,2}&\cdots&a_{1,n}b_{1,n}\\ a_{2,1}b_{2,1}&a_{2,2}b_{2,2}&\cdots&a_{2,n}b_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{m,1}b_{m,1}&a_{m,2}b_{m,2}&\cdots&a_{m,n}b_{m,n}\end{bmatrix}\]
- 克羅內積Kronnecker product： \[\mathbf A \otimes \mathbf B =\begin{bmatrix}a_{1,1}\mathbf B&a_{1,2}\mathbf B&\cdots&a_{1,n}\mathbf B\\ a_{2,1}\mathbf B&a_{2,2}\mathbf B&\cdots&a_{2,n}\mathbf B\\ \vdots&\vdots&\ddots&\vdots\\ a_{m,1}\mathbf B&a_{m,2}\mathbf B&\cdots&a_{m,n}\mathbf B \end{bmatrix}\]
$\mathbf {\vec x},\mathbf {\vec a},\mathbf {\vec b},\mathbf {\vec c}$ $n$ 階向量 $\mathbf A,\mathbf B,\mathbf C,\mathbf X$ $n$ 階方陣，則有： \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf {\vec x}) }{\partial \mathbf {\vec x} }=\frac{\partial(\mathbf {\vec x}^{T}\mathbf {\vec a}) }{\partial \mathbf {\vec x} } =\mathbf {\vec a}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X\mathbf {\vec b}) }{\partial \mathbf X }=\mathbf {\vec a}\mathbf {\vec b}^{T}=\mathbf {\vec a}\otimes\mathbf {\vec b}\in \mathbb R^{n\times n}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X^{T}\mathbf {\vec b}) }{\partial \mathbf X }=\mathbf {\vec b}\mathbf {\vec a}^{T}=\mathbf {\vec b}\otimes\mathbf {\vec a}\in \mathbb R^{n\times n}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X\mathbf {\vec a}) }{\partial \mathbf X }=\frac{\partial(\mathbf {\vec a}^{T}\mathbf X^{T}\mathbf {\vec a}) }{\partial \mathbf X }=\mathbf {\vec a}\otimes\mathbf {\vec a}\] \[\frac{\partial(\mathbf {\vec a}^{T}\mathbf X^{T}\mathbf X\mathbf {\vec b}) }{\partial \mathbf X }=\mathbf X(\mathbf {\vec a}\otimes\mathbf {\vec b}+\mathbf {\vec b}\otimes\mathbf {\vec a})\] \[\frac{\partial[(\mathbf A\mathbf {\vec x}+\mathbf {\vec a})^{T}\mathbf C(\mathbf B\mathbf {\vec x}+\mathbf {\vec b})]}{\partial \mathbf {\vec x}}=\mathbf A^{T}\mathbf C(\mathbf B\mathbf {\vec x}+\mathbf {\vec b})+\mathbf B^{T}\mathbf C(\mathbf A\mathbf {\vec x}+\mathbf {\vec a})\] \[\frac{\partial (\mathbf {\vec x}^{T}\mathbf A \mathbf {\vec x})}{\partial \mathbf {\vec x}}=(\mathbf A+\mathbf A^{T})\mathbf {\vec x}\] \[\frac{\partial[(\mathbf X\mathbf {\vec b}+\mathbf {\vec c})^{T}\mathbf A(\mathbf X\mathbf {\vec b}+\mathbf {\vec c})]}{\partial \mathbf X}=(\mathbf A+\mathbf A^{T})(\mathbf X\mathbf {\vec b}+\mathbf {\vec c})\mathbf {\vec b}^{T} \] \[\frac{\partial (\mathbf {\vec b}^{T}\mathbf X^{T}\mathbf A \mathbf X\mathbf {\vec c})}{\partial \mathbf X}=\mathbf A^{T}\mathbf X\mathbf {\vec b}\mathbf {\vec c}^{T}+\mathbf A\mathbf X\mathbf {\vec c}\mathbf {\vec b}^{T}\]
如 $f$ 是一元函式，則：
- 其逐元向量函式為 $f(\mathbf{\vec x}) =(f(x_1),f(x_2),\cdots,f(x_n))^{T}$ 。
- 其逐矩陣函式為： \[f(\mathbf X)=\begin{bmatrix} f(x_{1,1})&f(x_{1,2})&\cdots&f(x_{1,n})\\ f(x_{2,1})&f(x_{2,2})&\cdots&f(x_{2,n})\\ \vdots&\vdots&\ddots&\vdots\\ f(x_{m,1})&f(x_{m,2})&\cdots&f(x_{m,n})\\ \end{bmatrix}\]
- 其逐元導數分別為： \[f^{\prime}(\mathbf{\vec x}) =(f^{\prime}(x1),f^{\prime}(x2),\cdots,f^{\prime}(x_n))^{T}\\ f^{\prime}(\mathbf X)=\begin{bmatrix} f^{\prime}(x_{1,1})&f^{\prime}(x_{1,2})&\cdots&f^{\prime}(x_{1,n})\\ f^{\prime}(x_{2,1})&f^{\prime}(x_{2,2})&\cdots&f^{\prime}(x_{2,n})\\ \vdots&\vdots&\ddots&\vdots\\ f^{\prime}(x_{m,1})&f^{\prime}(x_{m,2})&\cdots&f^{\prime}(x_{m,n})\\ \end{bmatrix}\]
各種型別的偏導數：
- 標量對標量的偏導數 $\frac{\partial u}{\partial v}$ 。
- 標量對向量 $n$ 維向量）的偏導數 $\frac{\partial u}{\partial \mathbf {\vec v}}=(\frac{\partial u}{\partial v_1},\frac{\partial u}{\partial v_2},\cdots,\frac{\partial u}{\partial v_n})^{T}$ 。
- 標量對矩陣 $m\times n$ 階矩陣)的偏導數： \[\frac{\partial u}{\partial \mathbf V}=\begin{bmatrix} \frac{\partial u}{\partial V_{1,1}}&\frac{\partial u}{\partial V_{1,2}}&\cdots&\frac{\partial u}{\partial V_{1,n}}\\ \frac{\partial u}{\partial V_{2,1}}&\frac{\partial u}{\partial V_{2,2}}&\cdots&\frac{\partial u}{\partial V_{2,n}}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial u}{\partial V_{m,1}}&\frac{\partial u}{\partial V_{m,2}}&\cdots&\frac{\partial u}{\partial V_{m,n}} \end{bmatrix}\]
- 向量 $m$ 維向量）對標量的偏導數 $\frac{\partial \mathbf {\vec u}}{\partial v}=(\frac{\partial u_1}{\partial v},\frac{\partial u_2}{\partial v},\cdots,\frac{\partial u_m}{\partial v})^{T}$ 。
- 向量 $m$ 維向量）對向量 $n$ 維向量)的偏導數（雅可比矩陣，行優先） \[\frac{\partial \mathbf {\vec u}}{\partial \mathbf {\vec v}}=\begin{bmatrix} \frac{\partial u_1}{\partial v_1}&\frac{\partial u_1}{\partial v_2}&\cdots&\frac{\partial u_1}{\partial v_n}\\ \frac{\partial u_2}{\partial v_1}&\frac{\partial u_2}{\partial v_2}&\cdots&\frac{\partial u_2}{\partial v_n}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial u_m}{\partial v_1}&\frac{\partial u_m}{\partial v_2}&\cdots&\frac{\partial u_m}{\partial v_n} \end{bmatrix}\] 如果為列優先，則為上面矩陣的轉置。
- 矩陣 $m\times n$ 階矩陣)對標量的偏導數 \[\frac{\partial \mathbf U}{\partial v}=\begin{bmatrix} \frac{\partial U_{1,1}}{\partial v}&\frac{\partial U_{1,2}}{\partial v}&\cdots&\frac{\partial U_{1,n}}{\partial v}\\ \frac{\partial U_{2,1}}{\partial v}&\frac{\partial U_{2,2}}{\partial v}&\cdots&\frac{\partial U_{2,n}}{\partial v}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial U_{m,1}}{\partial v}&\frac{\partial U_{m,2}}{\partial v}&\cdots&\frac{\partial U_{m,n}}{\partial v} \end{bmatrix}\]
對於矩陣的跡，有下列偏導數成立： \[\frac{\partial [tr(f(\mathbf X))]}{\partial \mathbf X }=(f^{\prime}(\mathbf X))^{T}\] \[\frac{\partial [tr(\mathbf A\mathbf X\mathbf B)]}{\partial \mathbf X }=\mathbf A^{T}\mathbf B^{T} \] \[\frac{\partial [tr(\mathbf A\mathbf X^{T}\mathbf B)]}{\partial \mathbf X }=\mathbf B\mathbf A \] \[\frac{\partial [tr(\mathbf A\otimes\mathbf X )]}{\partial \mathbf X }=tr(\mathbf A)\mathbf I\] \[\frac{\partial [tr(\mathbf A\mathbf X \mathbf B\mathbf X)]}{\partial \mathbf X }=\mathbf A^{T}\mathbf X^{T}\mathbf B^{T}+\mathbf B^{T}\mathbf X \mathbf A^{T} \] \[\frac{\partial [tr(\mathbf X^{T} \mathbf B\mathbf X \mathbf C)]}{\partial \mathbf X }=(\mathbf B^{T}+\mathbf B)\mathbf X \mathbf C \mathbf C^{T} \] \[\frac{\partial [tr(\mathbf C^{T}\mathbf X^{T} \mathbf B\mathbf X \mathbf C)]}{\partial \mathbf X }=\mathbf B\mathbf X \mathbf C +\mathbf B^{T}\mathbf X \mathbf C^{T} \] \[\frac{\partial [tr(\mathbf A\mathbf X \mathbf B\mathbf X^{T} \mathbf C)]}{\partial \mathbf X }= \mathbf A^{T}\mathbf C^{T}\mathbf X\mathbf B^{T}+\mathbf C \mathbf A \mathbf X \mathbf B\] \[\frac{\partial [tr((\mathbf A\mathbf X\mathbf B+\mathbf C)(\mathbf A\mathbf X\mathbf B+\mathbf C))]}{\partial \mathbf X }= 2\mathbf A ^{T}(\mathbf A\mathbf X\mathbf B+\mathbf C)\mathbf B^{T}\]
假 $\mathbf U= f(\mathbf X)$ 是關 $\mathbf X$ 的矩陣值函式 $f:\mathbb R^{m\times n}\rightarrow \mathbb R^{m\times n}$ ）， $g(\mathbf U)$ 是關 $\mathbf U$ 的實值函式 $g:\mathbb R^{m\times n}\rightarrow \mathbb R $ ），則下面鏈式法則成立： \[\frac{\partial g(\mathbf U)}{\partial \mathbf X}= \left(\frac{\partial g(\mathbf U)}{\partial x_{i,j}}\right)_{m\times n}=\begin{bmatrix} \frac{\partial g(\mathbf U)}{\partial x_{1,1}}&\frac{\partial g(\mathbf U)}{\partial x_{1,2}}&\cdots&\frac{\partial g(\mathbf U)}{\partial x_{1,n}}\\ \frac{\partial g(\mathbf U)}{\partial x_{2,1}}&\frac{\partial g(\mathbf U)}{\partial x_{2,2}}&\cdots&\frac{\partial g(\mathbf U)}{\partial x_{2,n}}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial g(\mathbf U)}{\partial x_{m,1}}&\frac{\partial g(\mathbf U)}{\partial x_{m,2}}&\cdots&\frac{\partial g(\mathbf U)}{\partial x_{m,n}}\\ \end{bmatrix}\\ =\left(\sum_{k}\sum_{l}\frac{\partial g(\mathbf U)}{\partial u_{k,l}}\frac{\partial u_{k,l}}{\partial x_{i,j}}\right)_{m\times n}=\left(tr\left[\left(\frac{\partial g(\mathbf U)}{\partial \mathbf U}\right)^{T}\frac{\partial \mathbf U}{\partial x_{i,j}}\right]\right)_{m\times n}\]

概率論與隨機過程

一、概率與分佈

1.1 條件概率與獨立事件

條件概率：已 $A$ 事件發生的條件 $B$ 發生的概率，記 $P(B\mid A)$ ，它等於事 $AB$ 的概率相對於事 $A$ 的概率，即： \[P(B\mid A)=\frac {P(AB)}{P(A)}\] 其中必須 $P(A) \gt 0$
條件概率分佈的鏈式法則：對 $n$ 個隨機變 $\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n$ ，有： \[P(\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n)=P(\mathbf x_1)\prod_{i=2}^{n}P(\mathbf x_i \mid \mathbf x_1,\cdots,\mathbf x_{i-1})\]
兩個隨機變 $\mathbf x,\mathbf y$ 相互獨立的數學描述： \[\forall x\in \mathcal X,\forall y\in \mathcal Y, P(\mathbf x=x,\mathbf y=y)=P(\mathbf x=x)P(\mathbf y=y)\] 記作 $\mathbf x \bot \mathbf y$
兩個隨機變 $\mathbf x,\mathbf y$ 關於隨機變 $\mathbf z$ 條件獨立的數學描述： \[\forall x\in \mathcal X,\forall y\in \mathcal Y,\forall z \in\mathcal Z\\ P(\mathbf x=x,\mathbf y=y\mid \mathbf z=z)=P(\mathbf x=x\mid \mathbf z=z)P(\mathbf y=y\mid \mathbf z=z)\] 記作 $\mathbf x \bot \mathbf y \mid \mathbf z$

1.2 聯合概率分佈

定 ${\mathbf x}$ ${\mathbf y}$ 的聯合分佈為： \[P(a,b)=P\{{\mathbf x} \le a, {\mathbf y} \le b\}, - \infty \lt a,b \lt + \infty \]
${\mathbf x}$ 的分佈可以從聯合分佈中得到： \[ P_{\mathbf x}(a)=P\{{\mathbf x} \le a\}=P\{{\mathbf x} \le a, {\mathbf y} \le \infty\}=P(a,\infty), - \infty \lt a \lt + \infty \] 類似的 ${\mathbf y}$ 的分佈可以從聯合分佈中得到： \[ P_{\mathbf y}(b)=P\{{\mathbf y} \le b\}=P\{{\mathbf x} \le \infty, {\mathbf y} \le b\}=P(\infty,b), - \infty \lt b \lt + \infty \]
${\mathbf x}$ ${\mathbf y}$ 都是離散隨機變數時，定 ${\mathbf x}$ ${\mathbf y}$ 的聯合概率質量函式為 $p(x,y)=P\{{\mathbf x}=x,{\mathbf y}=y\}$ ${\mathbf x}$ ${\mathbf y}$ 的概率質量函式分佈為： \[p_{\mathbf x}(x)=\sum_{y \;:\;p(x,y) \gt 0}p(x,y) \\ p_{\mathbf y}(y)=\sum_{x \;:\;p(x,y) \gt 0}p(x,y)\]
${\mathbf x}$ ${\mathbf y}$ 聯合地連續時，即存在函 $p(x,y)$ ，使得對於所有的實數集 $A$ $B$ 滿足： \[P\{{\mathbf x} \in A, {\mathbf y} \in B\}=\int_B \int_A p(x,y) dx dy\] 則函 $p(x,y)$ 稱 ${\mathbf x}$ ${\mathbf y}$ 的概率密度函式。
- 聯合分佈為 \[P(a,b)=P\{{\mathbf x} \le a, {\mathbf y} \le b\}= \int_{-\infty}^{a} \int_{-\infty}^{b} p(x,y) dx dy\]
- ${\mathbf x}$ ${\mathbf y}$ 的概率密度函式以及分佈函式分別為： \[P_{\mathbf x}(a)=\int_{-\infty}^{a} \int_{-\infty}^{\infty} p(x,y) dx dy =\int_{-\infty}^{a} p_{\mathbf x}(x)dx\\ P_{\mathbf y}(b)=\int_{-\infty}^{\infty} \int_{-\infty}^{b} p(x,y) dx dy=\int_{-\infty}^{b} p_{\mathbf y}(y)dy\\ p_{\mathbf x}(x)=\int_{-\infty}^{\infty} p(x,y) dy\\ p_{\mathbf y}(y)=\int_{-\infty}^{\infty} p(x,y) dx\]

二、期望

期望：（是概率分佈的泛函，函式的函式）
- 離散型隨機變 ${\mathbf x}$ 的期望： \[\mathbb E[{\mathbf x}]=\sum_{i=1}^{\infty}x_ip_i\]
  - 若級數不收斂，則期望不存在
- 連續性隨機變 ${\mathbf x}$ 的期望： \[\mathbb E[{\mathbf x}]=\int_{-\infty}^{\infty}xp(x)dx\]
  - 若極限不收斂，則期望不存在
期望描述了隨機變數的平均情況，衡量了隨機變 ${\mathbf x}$ 的均值
定理： ${\mathbf y}=g({\mathbf x})$ 均為隨機變數 $g(\cdot)$ 是連續函式
- ${\mathbf x}$ 為離散型隨機變數， ${\mathbf y}$ 的期望存在，則： \[\mathbb E[{\mathbf y}]=\mathbb E[g({\mathbf x})]=\sum_{i=1}^{\infty}g(x_i)p_i\]
- ${\mathbf x}$ 為連續型隨機變數， ${\mathbf y}$ 的期望存在，則： \[\mathbb E[{\mathbf y}]=\mathbb E[g({\mathbf x})]=\int_{-\infty}^{\infty}g(x)p(x)dx\] 該定理的意義在於：當 $\mathbb E({\mathbf y})$ 時，不必計算 ${\mathbf y}$ 的分佈，只需要利 ${\mathbf x}$ 的分佈即可。該定理可以推廣至兩個或者兩個以上隨機變數的情況。此時： \[ \mathbb E[Z]=\mathbb E[g({\mathbf x},{\mathbf y})]=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(x,y)p(x,y)dxdy\]
  
  上述公式也記做： \[\mathbb E_{\mathbf x\sim P}[g(x)]=\sum_{x}g(x)p(x)\\ \mathbb E_{\mathbf x\sim P}[g(x)]=\int g(x)p(x)dx\\ \mathbb E_{\mathbf x,\mathbf y\sim P}[g(x)]\int g(x,y)p(x,y)dxdy\]
期望性質：
- 常數的期望就是常數本身
- 對常 $C$ 有： \[\mathbb E[C{\mathbf x}]=C\mathbb E[{\mathbf x}]\]
- 對兩個隨機變 ${\mathbf x},{\mathbf y}$ ，有： \[\mathbb E[{\mathbf x}+{\mathbf y}]=\mathbb E[{\mathbf x}]+\mathbb E[{\mathbf y}]\]
  - 該結論可以推廣到任意有限個隨機變數之和的情況
- 對兩個相互獨立的隨機變數，有： \[\mathbb E[{\mathbf x}{\mathbf y}]=\mathbb E[{\mathbf x}]\mathbb E[{\mathbf y}]\]
  - 該結論可以推廣到任意有限個相互獨立的隨機變數之積的情況

三、方差

3.1 方差

對隨機變 ${\mathbf x}$ ， $\mathbb E[({\mathbf x}-\mathbb E[{\mathbf x}])^{2}]$ 存在，則稱它 ${\mathbf x}$ 的方差，記 $Var[{\mathbf x}]$ ${\mathbf x}$ 的標準差為方差的開平方。即： \[Var[{\mathbf x}]=\mathbb E[({\mathbf x}-\mathbb E[{\mathbf x}])^{2}] \\ \sigma=\sqrt{Var[{\mathbf x}]}\]
- 方差度量了隨機變數 ${\mathbf x}$ 與期望值偏離的程度，衡量了 ${\mathbf x}$ 取值分散程度的一個尺度。
- 由於絕對值 $|{\mathbf x}-\mathbb E[{\mathbf x}] |$ 帶有絕對值，不方便運算，因此採用平方來計算。又因為 $|{\mathbf x}-\mathbb E[{\mathbf x}]|^2$ 是一個隨機變數，因此對它取期望，即得 ${\mathbf x}$ 與期望值偏離的均值
根據定義可知： \[Var[{\mathbf x}]=\mathbb E[({\mathbf x}-\mathbb E[{\mathbf x}])^{2}]=\mathbb E[{\mathbf x}^{2}]-(\mathbb E[{\mathbf x}])^{2}\\ Var [f(\mathbf x)]=\mathbb E[(f(\mathbf x)-\mathbb E[f(\mathbf x)])^{2}]\]
對於一個期望 $\mu$ ，方差 $\sigma^{2},\sigma \ne 0$ 的隨機變 ${\mathbf x}$ ，隨機變 ${\mathbf x}^{*}=\frac {{\mathbf x}-\mu}{\sigma}$ 的數學期望為0，方差為1。 ${\mathbf x}^{\ast}$ ${\mathbf x}$ 的標準化變數
方差的性質：
- 常數的方差恆為0
- 對常 $C$ $Var[C{\mathbf x}]=C^{2}Var[{\mathbf x}]$
- 對兩個隨機變 ${\mathbf x},{\mathbf y}$ ，有 $Var[{\mathbf x}+{\mathbf y}]=Var[{\mathbf x}] +Var[{\mathbf y}] +2\mathbb E[({\mathbf x}-\mathbb E[{\mathbf x}])({\mathbf y}-\mathbb E[{\mathbf y}])] $
  - 當 ${\mathbf x}$ 和 ${\mathbf y}$ 相互獨立時，有 $Var[{\mathbf x}+{\mathbf y}] = Var[{\mathbf x}] +Var[{\mathbf y}] $ 。可以推廣至任意有限多個相互獨立的隨機變數之和的情況
- $Var [{\mathbf x}] =0$ 的充要條件 ${\mathbf x}$ 以概率1取常數

3.2 協方差與相關係數

對於二維隨機變 $({\mathbf x},{\mathbf y})$ ，可以討論描 ${\mathbf x}$ ${\mathbf y}$ 之間相互關係的數字特徵。
- 定義 $\mathbb E[({\mathbf x}-\mathbb E[{\mathbf x}])({\mathbf y}-\mathbb E [{\mathbf y}])] $ 為隨機變數 ${\mathbf x}$ 與 ${\mathbf y}$ 的協方差，記作 $ Cov[ {\mathbf x},{\mathbf y}]=\mathbb E[({\mathbf x}-\mathbb E[{\mathbf x}])({\mathbf y}-\mathbb E [{\mathbf y}])]$ 。
- 定義 $\rho_{{\mathbf x}{\mathbf y}}=\frac {Cov[{\mathbf x},{\mathbf y}]}{\sqrt{Var[{\mathbf x}] }\sqrt{Var[{\mathbf y}]}}$ 為隨機變數 ${\mathbf x}$ 與 ${\mathbf y}$ 　的相關係數，它是協方差的歸一化。
由定義可知： \[Cov[ {\mathbf x},{\mathbf y}] =Cov[ {\mathbf y},{\mathbf x}] \\ Cov [{\mathbf x},{\mathbf x}] =Var [{\mathbf x}] \\ Var [{\mathbf x}+{\mathbf y}] =Var [{\mathbf x}] +Var [{\mathbf y}] +2Cov [{\mathbf x},{\mathbf y}] \]
協方差的性質：
- $Cov [a{\mathbf x},b{\mathbf y}] =abCov [{\mathbf x},{\mathbf y}] $ , $a,b$ 為常數
- $Cov[ {\mathbf x}_1+{\mathbf x}_2,{\mathbf y} ]=Cov [{\mathbf x}_1,{\mathbf y}] +Cov [{\mathbf x}_2,{\mathbf y}] $
- $Cov [f(\mathbf x),g(\mathbf y)]=\mathbb E[(f(\mathbf x)-\mathbb E[f(\mathbf x)])(g(\mathbf y)-\mathbb E[g(\mathbf y)])]$
- $\rho[f(\mathbf x),g(\mathbf y)]=\frac {Cov[f(\mathbf x),g(\mathbf y)]}{\sqrt{Var[f(\mathbf x)] }\sqrt{Var[g(\mathbf y)]}}$
協方差的物理意義：
- 協方差的絕對值越大，說明兩個隨機變數都遠離它們的均值。
- 協方差如果為正，則說明兩個隨機變數同時趨向於取較大的值；如果為負，則說明一個隨變數趨向於取較大的值，另一個隨機變數趨向於取較小的值
- 兩個隨機變數的獨立性可以匯出協方差為零。但是兩個隨機變數的協方差為零無法匯出獨立性
  - 因為獨立性也包括：沒有非線性關係。有可能兩個隨機變數是非獨立的，但是協方差為零
  - 假設隨機變 $\mathbf x\sim U[-1,1]$ 。定義隨機變 $\mathbf s$ 的概率分佈函式為： \[P(\mathbf s=1)= \frac 12P(\mathbf s=-1)= \frac 12 \] 定義隨機變 $\mathbf y=\mathbf {sx}$ ，則隨機變 $\mathbf x,\mathbf y$ 是非獨立的，但是有 $Cov[\mathbf x,\mathbf y]=0$
相關係數的物理意義：考慮以隨機變 ${\mathbf x}$ 的線性函 $a+b{\mathbf x}$ 來近似表 ${\mathbf y}$ 。以均方誤差 \[e=\mathbb E[({\mathbf y}-(a+b{\mathbf x}))^{2}]=\mathbb E[{\mathbf y}^{2}] +b^{2}\mathbb E[{\mathbf x}^{2}] +a^{2}-2b\mathbb E[{\mathbf x}{\mathbf y}] +2ab\mathbb E[{\mathbf x}] -2a\mathbb E [{\mathbf y}] \] 來衡量 $a+b{\mathbf x}$ 近似表 ${\mathbf y}$ 的好壞程度 $e$ 越小表示近似程度越高。為求得最好的近似，則 $a,b$ 分別取偏導數，得到： \[a_0=\mathbb E[{\mathbf y}] -b_0\mathbb E[{\mathbf x}] =\mathbb E[{\mathbf y}] -\mathbb E[{\mathbf x}] \frac{Cov [{\mathbf x},{\mathbf y}]}{Var [{\mathbf x}] }\\ b_0=\frac{Cov[ {\mathbf x},{\mathbf y}] }{Var[ {\mathbf x}] }\\ \min(e)=\mathbb E[({\mathbf y}-(a_0+b_0{\mathbf x}))^{2}]=(1-\rho^{2}_{{\mathbf x}{\mathbf y}})Var [{\mathbf y}] \] 因此有以下定理：
- $|\rho_{{\mathbf x}{\mathbf y}}| \le 1$ $|...|$ 是絕對值）
- $|\rho_{{\mathbf x}{\mathbf y}}| = 1$ 的充要條件是，存在常數 $a,b$ 使得 $P\{{\mathbf y}=a+b{\mathbf x}\}=1$
  
  $|\rho_{{\mathbf x}{\mathbf y}}|$ 較大時 $e$ 較小，表明隨機變 ${\mathbf x}$ ${\mathbf y}$ 聯絡較緊密，於 $\rho_{{\mathbf x}{\mathbf y}}$ 是一個表 ${\mathbf x}$ ${\mathbf y}$ 之間線性關係緊密程度的量。
$\rho_{{\mathbf x}{\mathbf y}}=0$ 時， ${\mathbf x}$ ${\mathbf y}$ 不相關。
- 不相關是就線性關係來講的，而相互獨立是一般關係而言的。
- 相互獨立一定不相關；不相關則未必獨立。

3.3 協方差矩陣

矩： ${\mathbf x}$ ${\mathbf y}$ 是隨機變數
- 若 $\mathbb E[{\mathbf x}^{k}] ,k=1,2,\cdots$ 存在，則稱它為 ${\mathbf x}$ 的 $k$ 階原點矩，簡稱 $k$ 階矩
- 若 $\mathbb E[({\mathbf x}-\mathbb E[{\mathbf x}])^{k}] ,k=2,3,\cdots$ 存在，則稱它為 ${\mathbf x}$ 的 $k$ 階中心矩
- 若 $\mathbb E[{\mathbf x}^{k}{\mathbf y}^{l}] ,k,l=1,2,\cdots$ 存在，則稱它為 ${\mathbf x}$ 和 ${\mathbf y}$ 的 $ k+l$ 階混合矩
- 若 $\mathbb E[({\mathbf x}-\mathbb E[{\mathbf x}])^{k}({\mathbf y}-\mathbb E[{\mathbf y}])^{l}] ,k,l=1,2,\cdots$ 存在，則稱它為 ${\mathbf x}$ 和 ${\mathbf y}$ 的 $k+l$ 階混合中心矩因此期望是一階原點矩，方差是二階中心矩，協方差是二階混合中心矩
協方差矩陣：二維隨機變 $({\mathbf x}_1,{\mathbf x}_2)$ 有四個二階中心矩（設他們都存在），記作： \[\begin{align} c_{11}&=\mathbb E[({\mathbf x}_1-\mathbb E[{\mathbf x}_1])^{2}] \\ c_{12}&=\mathbb E[({\mathbf x}_1-\mathbb E[{\mathbf x}_1])( {\mathbf x}_2-\mathbb E[{\mathbf x}_2]) ] \\ c_{21}&=\mathbb E[( {\mathbf x}_2-\mathbb E[{\mathbf x}_2])({\mathbf x}_1-\mathbb E[{\mathbf x}_1] ) ] \\ c_{22}&=\mathbb E[({\mathbf x}_2-\mathbb E[{\mathbf x}_2])^{2}] \\ \end{align}\] 這個矩陣稱作隨機變 $({\mathbf x}_1,{\mathbf x}_2)$ 的協方差矩陣。 $n$ 維隨機變 $({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n)$ 的二階混合中心 $c_{ij}=Cov [{\mathbf x}_i,{\mathbf x}_j] =\mathbb E[({\mathbf x}_i-\mathbb E[{\mathbf x}_i] )( {\mathbf x}_j-\mathbb E[{\mathbf x}_j] ) ] ,i,j=1,2,\cdots,n$ ,都存在，則稱矩陣 \[\mathbf C= \begin{bmatrix} c_{11} & c_{12} & \cdots & c_{1n} \\ c_{21} & c_{22} & \cdots & c_{2n} \\ \vdots &\vdots &\ddots &\vdots \\ c_{n1} & c_{n2} & \cdots & c_{nn} \\ \end{bmatrix}\] $n$ 維隨機變 $({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n)$ 的協方差矩陣。
- 由於 $c_{ij}=c_{ji}, i\ne j, i,j=1,2,\cdots,n$ 因此協方差矩陣是個對稱陣
  
  通 $n$ 維隨機變數的分佈是不知道的，或者太複雜以致數學上不容易處理。因此實際中協方差矩陣非常重要。

四、大數定律及中心極限定理

4.1 切比雪夫不等式

切比雪夫不等式：隨機變 ${\mathbf x}$ 具有期 $\mathbb E[{\mathbf x}] =\mu$ ，方 $Var({\mathbf x})=\sigma^{2}$ ,對於任意正 $\varepsilon$ ，不等式 \[P\{|{\mathbf x}-\mu| \ge \varepsilon\} \le \frac {\sigma^{2}}{\varepsilon^{2}}\] 成立

其意義是：對於距 $\mathbb E[{\mathbf x}] $ 足夠遠的地方（距離大於等 $\varepsilon$ ），事件出現的概率是小於等 $ \frac {\sigma^{2}}{\varepsilon^{2}}$ ；即事件出現在區 $[\mu-\varepsilon , \mu+\varepsilon]$ 的概率大 $1- \frac {\sigma^{2}}{\varepsilon^{2}}$ 該不等式給出了隨機變 ${\mathbf x}$ 在分佈未知的情況下，事 $\{|{\mathbf x}-\mu| \le \varepsilon\}$ 的下限估計（ $P\{|{\mathbf x}-\mu| \lt 3\sigma\} \ge 0.8889$ 證明： \[P\{|{\mathbf x}-\mu| \ge \varepsilon\}=\int_{|x-\mu| \ge \varepsilon}p(x)dx \le \int_{|x-\mu| \ge \varepsilon} \frac{|x-\mu|^{2}}{\varepsilon^{2}}p(x)dx \\ \le \frac {1}{\varepsilon^{2}}\int_{-\infty}^{\infty}(x-\mu)^{2}p(x)dx=\frac{\sigma^{2}}{\varepsilon^{2}}\]
切比雪夫不等式的特殊情況：設隨機變 ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n,\cdots$ 相互獨立，且具有相同的數學期望和方差 $ \mathbb E[{\mathbf x}_k] =\mu, Var[{\mathbf x}_k] =\sigma^{2},k=1,2,\cdots$ 。作 $n$ 個隨機變數的算術平均 $ \overline {\mathbf x} =\frac {1}{n} \sum _{k=1}^{n}{\mathbf x}_k$ ，則對於任意正 $ \varepsilon$ 有： \[\lim_{n\rightarrow \infty}P\{|\overline {\mathbf x}-\mu| \lt \varepsilon\}=\lim_{n\rightarrow \infty}P\{|\frac{1}{n}\sum_{k=1}^{n}{\mathbf x}_k-\mu| \lt \varepsilon\} =1\] 證明： \[\mathbb E[\frac{1}{n}\sum_{k=1}^{n}{\mathbf x}_k]=\mu\\ Var[\frac{1}{n}\sum_{k=1}^{n}{\mathbf x}_k]=\frac{\sigma^{2}}{n}\] 有切比雪夫不等式，以 $n$ 趨於無窮時，可以證明。詳細過程省略

4.2 大數定理

依概率收斂： ${\mathbf y}_1,{\mathbf y}_2,\cdots,{\mathbf y}_n,\cdots$ 是一個隨機變數序列 $a$ 是一個常數。若對於任意正 $ \varepsilon$ 有 $\lim_{n\rightarrow \infty}P\{|{\mathbf y}_{n}-a| \le \varepsilon \}=1$ ,則稱序 ${\mathbf y}_1,{\mathbf y}_2,\cdots,{\mathbf y}_n,\cdots$ 依概率收斂 $a$ 。記作 ${\mathbf y}_{n} \stackrel{P}{\rightarrow} a$
依概率收斂的兩個含義：
- 收斂：表明這是一個隨機變數序列，而不是某個隨機變數；且序列是無限長，而不是有限長
- 依概率：表明序列無窮遠處的隨機變數 ${\mathbf y}_{\infty}$ 的分佈規律為：絕大部分分佈於點 $a$ ，極少數位於 $a$ 之外。且分佈於 $a$ 之外的事件發生的概率之和為0
大數定理一：設隨機變 ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n,\cdots$ 相互獨立，且具有相同的數學期望和方差 $ \mathbb E[{\mathbf x}_k] =\mu, Var[{\mathbf x}_k] =\sigma^{2},k=1,2,\cdots$ 。則序列 $ \overline {\mathbf x} =\frac {1}{n} \sum _{k=1}^{n}{\mathbf x}_k$ 依概率收斂 $\mu$ ， $\overline {\mathbf x} \stackrel{P}{\rightarrow} \mu$
- 這裡並沒有要求隨機變數 ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n,\cdots$ 同分布
伯努利大數定理： $n_A$ $n$ 次獨立重複實驗中事 $A$ 發生的次數 $p$ 是事 $A$ 在每次試驗中發生的概率。則對於任意正 $ \varepsilon$ 有： \[\lim_{n \rightarrow \infty}P\{|\frac{n_{A}}{n}-p| \lt \varepsilon\}=1 \\ or: \quad \lim_{n \rightarrow \infty}P\{|\frac{n_{A}}{n}-p| \ge \varepsilon\}=0\]
- 即：當獨立重複實驗執行非常大的次數時，事件 $A$ 發生的頻率逼近於它的概率
辛欽定理：設隨機變 ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n,\cdots$ 相互獨立，服從同一分佈，且具有相同的數學期望 $ \mathbb E[{\mathbf x}_k] =\mu,k=1,2,\cdots$ 。則對於任意正 $ \varepsilon$ 有： \[\lim_{n\rightarrow \infty}P\{|\frac{1}{n}\sum_{k=1}^{n}{\mathbf x}_k-\mu| \lt \varepsilon\} =1\]
- 這裡並沒有要求隨機變數 ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n,\cdots$ 的方差存在
- 伯努利大數定理是親欽定理的特殊情況。

4.3 中心極限定理

獨立同分布的中心極限定理：設隨機變 ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n$ 獨立同分布，且具有數學期望和方差 $\mathbb E[{\mathbf x}_k] =\mu, Var[{\mathbf x}_k] =\sigma^{2} \gt 0,k=1,2,\cdots$ ，則隨機變數之 $\overline {S{\mathbf x}_n}=\sum_{k=1}^{n} {\mathbf x}_k$ 的標準變化量: \[{\mathbf y}_n=\frac{\overline {S{\mathbf x}_n}-\mathbb E[\overline {S{\mathbf x}_n}] }{\sqrt{Var[\overline {S{\mathbf x}_n}] }}=\frac{\overline {S{\mathbf x}_n}-n\mu}{\sqrt n \sigma}\] 的概率分佈函 $F_n(x)$ 對於任 $x$ 滿足： \[\lim_{n\rightarrow \infty}F_n(x)=\lim_{n\rightarrow \infty}P\{{\mathbf y}_n \le x\}\\ =\lim_{n\rightarrow \infty}P\{\frac{\sum_{k=1}^{n} {\mathbf x}_k-n\mu}{\sqrt n \sigma} \le x\}\\ = \int_{-\infty}^{x} \frac{1}{\sqrt{2\pi}}e^{-t^{2}/2}dt=\Phi(x)\]
- 其物理意義為：均值方差為 $\mu,\sigma^{2}$ 的獨立同分布的隨機變數 ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n$ 之和 $\overline {S{\mathbf x}_n}=\sum_{k=1}^{n} {\mathbf x}_k$ 的標準變化量 ${\mathbf y}_n$ ，當 $n$ 充分大時，其分佈近似與標準正態分佈。即 $\overline {S{\mathbf x}_n}=\sum_{k=1}^{n} {\mathbf x}_k$ 在 $n$ 充分大時，其分佈近似於 $N(n\mu,n\sigma^{2})$
- 一般情況下，很難求出 $n$ 個隨機變數之和的分佈函式。因此當 $n$ 充分大時，可以通過正態分佈來做理論上的分析或者計算。
Liapunov定理：設隨機變 ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n,\cdots$ 相互獨立，具有數學期望和方差 $\mathbb E[{\mathbf x}_k] =\mu_k,Var[{\mathbf x}_k] =\sigma_k^{2} \gt 0, k=1,2,\cdots$ ，記 $B_n^{2}=\sum_{k=1}^{n}\sigma_k^{2}$ 。若存在正 $\delta$ ，使得 $n \rightarrow \infty$ 時， \[\frac{1}{B_n^{2+\delta}}\sum_{k=1}^{n}\mathbb E [|{\mathbf x}_k-\mu_k|^{2+\delta}] \rightarrow 0\] 則隨機變數之 $\overline {S{\mathbf x}_n}=\sum_{k=1}^{n} {\mathbf x}_k$ 的標準變化量: \[Z_n=\frac{\overline {S{\mathbf x}_n}-\mathbb E[\overline {S{\mathbf x}_n}] }{\sqrt{Var [\overline {S{\mathbf x}_n}] }}=\frac{\overline {S{\mathbf x}_n}-\sum_{k=1}^{n}\mu_k}{B_n}\] 的概率分佈函 $F_n(x)$ 對於任 $x$ 滿足： \[\lim_{n\rightarrow \infty}F_n(x)=\lim_{n\rightarrow \infty}P\{Z_n \le x\}\\ =\lim_{n\rightarrow \infty}P\{\frac{\sum_{k=1}^{n} {\mathbf x}_k-\sum_{k=1}^{n}\mu_k}{B_n} \le x\}\\ = \int_{-\infty}^{x} \frac{1}{\sqrt{2\pi}}e^{-t^{2}/ 2}dt=\Phi(x)\]
- 其物理意義為：相互獨立的隨機變數 ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n,\cdots$ 之和 $\overline {S{\mathbf x}_n}=\sum_{k=1}^{n} {\mathbf x}_k$ 的衍生隨機變數序 $Z_n=\frac{\overline {S{\mathbf x}_n}-\sum_{k=1}^{n}\mu_k}{B_n}$ ，當 $n$ 充分大時，其分佈近似與標準正態分佈。
- 這裡並不要求 ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n,\cdots$ 同分布
Demoiver-Laplace定理：設隨機變數序 $\eta_n,n=1,2,...$ 服從引數 $n, p(0 \lt p \lt 1)$ 的二項分佈，則對於任 $x$ ,有： \[\lim_{n\rightarrow \infty}P\{\frac{\eta_n-np}{\sqrt{np(1-p)}} \le x\}=\int_{-\infty}^{x} \frac{1}{\sqrt{2\pi}}e^{-t^{2}\mid 2}dt=\Phi(x)\]
- 該定理表明，正態分佈是二項分佈的極限分佈。當 $n$ 充分大時，可以利用正態分佈來計算二項分佈的概率。

五、不確定性來源

機器學習中不確定性有三個來源:
- 模型本身固有的隨機性。如量子力學中的粒子動力學方程。
- 不完全的觀測。即使是確定性系統，當無法觀測所有驅動變數時，結果也是隨機的。
- 不完全建模。有時必須放棄一些觀測資訊。
  - 如機器人建模中：雖然可以精確觀察機器人周圍每個物件的位置；但在預測這些物件將來的位置時，對空間進行了離散化。則位置預測將帶有不確定性。

六、常見概率分佈

6.1 均勻分佈

離散隨機變數的均勻分佈：假 $\mathbf x$ $k$ 個取值 $x_1,x_2,\cdots,x_k$ ，則均勻分佈的概率密度函式(probability mass function:PMF)為： \[P(\mathbf x=x_i) =\frac 1k,\quad i=1,2,\cdots,k\]
連續隨機變數的均勻分佈：假 $\mathbf x$ 在[a,b]上均勻分佈，則其概率密度函式(probability density function：PDF)為： \[p(\mathbf x=x)=\begin{cases} 0,&x\notin [a,b]\\ \frac{1}{b-a},&x \in [a,b]\\ \end{cases} \]

6.2 二項分佈

伯努利分佈（二項分佈）：引數 $\phi\in [0,1]$ 。隨機變 $\mathbf x \in \{0,1\}$
- 概率分佈函式為： \[P(\mathbf x=x)=\phi^{x}(1-\phi)^{1-x}\;,x \in \{0,1\}\]
- 期望： $\mathbb E_{\mathbf x}[x]=\phi$
- 方差： $Var_{\mathbf x}[x]=\phi(1-\phi)$
categorical分佈：它是二項分佈的推廣，也稱作multinoulli分佈。假設隨機變 $\mathbf x \in \{1,2,\cdots,K\}$ ，其概率分佈函式為： \[P(\mathbf x=1)=\theta_1\\ P(\mathbf x=2)=\theta_2\\ \vdots\\ P(\mathbf x=K-1)=\theta_{K-1}\\ P(\mathbf x=K)=1-\sum_{i=1}^{K-1}\theta_i \\\] 其 $\theta_i$ 為引數，它滿 $\theta_i \in [0,1]$ ， $\sum_{i=1}^{K-1}\theta_i \in [0,1]$ 。

6.3 高斯分佈

6.3.1 一維正態分佈

正態分佈的概率密度函式為: \[p(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-(x-\mu)^{2}/ (2\sigma^{2})}, -\infty \lt x \lt \infty\] 其 $\mu,\sigma(\sigma \gt 0) $ 為常數。
- 若隨機變數 ${\mathbf x}$ 的概率密度函式如上所述，則稱 ${\mathbf x}$ 服從引數為 $\mu,\sigma$ 的正態分佈或者高斯分佈，記作 ${\mathbf x} \sim N(\mu,\sigma^{2})$ 。
- 特別的，當 $\mu=0,\sigma=1$ 時，稱為標準正態分佈，其概率密度函式記作 $\varphi(x)$ , 分佈函式記作 $\Phi(x)$
為了計算方便，有時也記作： \[\mathcal N(x;\mu,\beta^{-1}) =\sqrt{\frac{\beta}{2\pi}}\exp\left(-\frac{1}{2}\beta(x-\mu)^{2}\right)\] 其 $\beta \in (0,\infty)$
- 正態分佈是很多應用中的合理選擇。如果某個隨機變數取值範圍是實數，且對它的概率分佈一無所知，通常會假設它服從正態分佈。有兩個原因支援這一選擇：
- 建模的任務的真實分佈通常都確實接近正態分佈。中心極限定理表明，多個獨立隨機變數的和近似正態分佈。
- 在具有相同方差的所有可能的概率分佈中，正態分佈的熵最大（即不確定性最大）。
正態分佈的概率密度函式性質：
- 曲線關於 $x=\mu$ 對稱
- 曲線在 $x=\mu$ 時取最大值
- 曲線在 $x=\mu \pm \sigma $ 處有拐點
  
  參 $\mu$ 決定曲線的位置 $\sigma$ 決定圖形的胖瘦
${\mathbf x} \sim N(\mu,\sigma^{2})$ 則 $\frac{{\mathbf x}-\mu}{\sigma} \sim N(0,1)$
有限個相互獨立的正態隨機變數的線性組合仍然服從正態分佈。
正態分佈的期望就 $\mu$ ，方差就 $\sigma^{2}$
若隨機變 ${\mathbf x}_i \sim N(\mu_i,\sigma_i^{2}),i=1,2,\cdots,n$ 且它們相互獨立，則它們的線性組合： $C_1{\mathbf x}_1+C_2{\mathbf x}_2+\cdots+C_n{\mathbf x}_n$ 其中 $C_1,C_2,\cdots,C_n$ 不全是為0的常數）仍然服從正態分佈，且： \[C_1{\mathbf x}_1+C_2{\mathbf x}_2+\cdots+C_n{\mathbf x}_n \sim N(\sum_{i=1}^{n}C_i\mu_i,\sum_{i=1}^{n}C_i^{2}\sigma_i^{2})\]

6.3.2 多維正態分佈

二維正態隨機變 $({\mathbf x}_1,{\mathbf x}_2)$ 的概率密度為： \[p(x_1,x_2)=\\ \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^{2}}}\exp\{\frac{-1}{2(1-\rho^{2})}[\frac{(x_1-\mu_1)^{2}}{\sigma_1^{2}}-2\rho\frac{(x_1-\mu_1)(x_2-\mu_2)}{\sigma_1\sigma_2}+\frac{(x_2-\mu_2)^{2}}{\sigma_2^{2}}]\}\] 可以計算出: \[p_{\mathbf x}(x)=\frac{1}{\sqrt{2\pi}\sigma_1}e^{-(x-\mu_1)^{2}/ (2\sigma_1^{2})}, -\infty \lt x \lt \infty \\ p_{\mathbf y}(y)=\frac{1}{\sqrt{2\pi}\sigma_2}e^{-(y-\mu_2)^{2}/ (2\sigma_2^{2})}, -\infty \lt y \lt \infty\\ \mathbb E[{\mathbf x}] =\mu_1 \\ \mathbb E[{\mathbf y}] =\mu_2 \\ Var[{\mathbf x}] =\sigma_1^{2} \\ Var[{\mathbf y}]=\sigma_2^{2}\\ Cov[{\mathbf x},{\mathbf y}]=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}(x-\mu_1)(y-\mu_2)p(x,y)dxdy=\rho \sigma_1\sigma_2\\ \rho_{{\mathbf x}{\mathbf y}}=\rho\]
引入矩陣： \[\mathbf{\vec {\mathbf x}}=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \quad \mathbf{\vec \mu}=\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}\\ \mathbf{\Sigma}=\begin{bmatrix} c_{11} &c_{12}\\ c_{21} &c_{22} \end{bmatrix} = \begin{bmatrix} \sigma_1^{2} & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^{2} \end{bmatrix}\] $\mathbf \Sigma$ $({\mathbf x}_1,{\mathbf x}_2)$ 的協方差矩陣。其行列式 $\det \mathbf{\Sigma} =\sigma_1^{2}\sigma_2^{2}(1-\rho^{2})$ ，其逆矩陣為： \[\mathbf{\Sigma}^{-1}=\frac{1}{\det\mathbf \Sigma}\begin{bmatrix} \sigma_2^{2} & -\rho \sigma_1 \sigma_2 \\ -\rho \sigma_1 \sigma_2 & \sigma_1^{2} \end{bmatrix}\] 於 $({\mathbf x}_1,{\mathbf x}_2)$ 的概率密度函式可以寫 $( \mathbf {\vec {\mathbf x}}- \mathbf {\vec \mu})^{T}$ 表示矩陣的轉置： \[p(x_1,x_2)=\frac{1}{(2\pi)(\det \mathbf \Sigma)^{1/ 2}}\exp\{- \frac 12 ( \mathbf {\vec {\mathbf x}}- \mathbf {\vec \mu})^{T} \mathbf \Sigma^{-1}( \mathbf {\vec {\mathbf x}}- \mathbf {\vec \mu})\}\] 其中均 $\mu_1,\mu_2$ 決定了曲面的位置（本例中均值都為0）。標準 $\sigma_1,\sigma_2$ 決定了曲面的陡峭程度（本例中方差都為1）。 $\rho$ 決定了協方差矩陣的形狀，從而決定了曲面的形狀
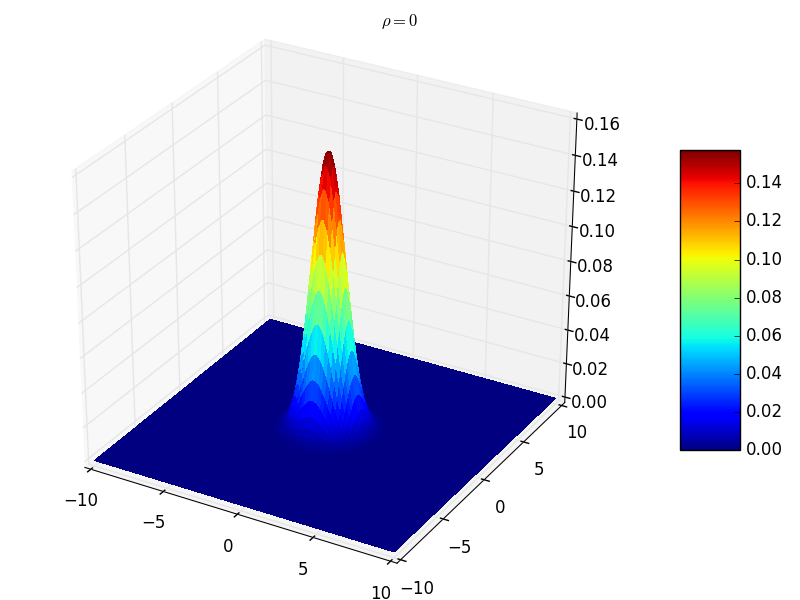
- $\rho=0$ 時，協方差矩陣對角線非零，其他位置均為零。此時表示隨機變數之間不相關。此時的聯合分佈概率函式形狀如下圖所示，曲面在 $z=0$ 平面的截面是個圓形：
- $\rho=0.5$ 時，協方差矩陣對角線非零，其他位置均為零。此時表示隨機變數之間相關。此時的聯合分佈概率函式形狀如下圖所示，曲面在 $z=0$ 平面的截面是個橢圓，相當於圓形沿著直線 $y=x$ 方向壓縮：
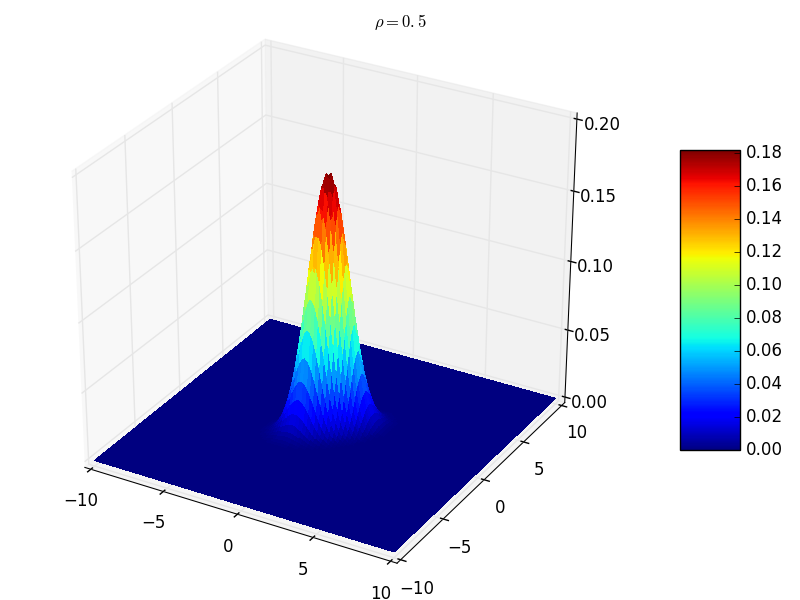
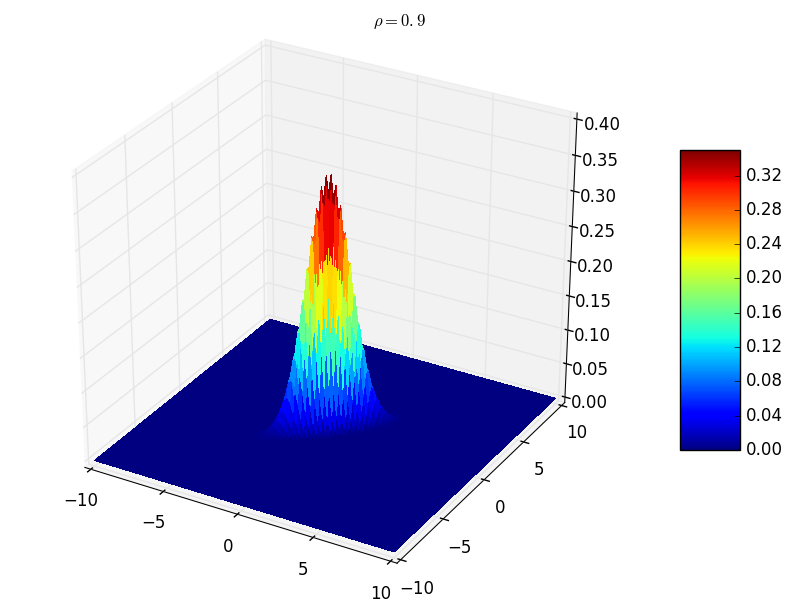
- $\rho=1$ 時，協方差矩陣對角線非零，其他位置均為零。此時表示隨機變數之間完全相關。此時的聯合分佈概率函式形狀為：曲面在 $z=0$ 平面的截面是直線 $y=x$ ，相當於圓形沿著直線 $y=x$ 方向壓縮成一條直線。由於 $\rho=1$ 會導致除數為 0，因此這裡給出 $\rho=0.9$ ：
多維正態隨機變 $({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n)$ ，引入列矩陣： \[\mathbf{\vec {\mathbf x}}=\begin{bmatrix} x_1 \\ x_2 \\ \vdots\\ x_n \end{bmatrix} \quad \mathbf{\vec \mu}=\begin{bmatrix} \mu_1 \\ \mu_2\\ \vdots\\ \mu_n \end{bmatrix}=\begin{bmatrix} \mathbb E[{\mathbf x}_1] \\ \mathbb E[{\mathbf x}_2] \\ \vdots\\ \mathbb E[{\mathbf x}_n] \end{bmatrix}\] $\mathbf \Sigma$ $({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n)$ 的協方差矩陣。則 \[p(x_1,x_2,x_3,\cdots,x_n)=\frac {1}{(2\pi)^{n/2}(\det \mathbf \Sigma)^{1/2}} \exp \{- \frac 12( \mathbf {\vec {\mathbf x}}- \mathbf {\vec \mu})^{T}\mathbf \Sigma^{-1}( \mathbf {\vec {\mathbf x}}- \mathbf {\vec \mu})\}\] 記做 \[\mathcal N(\mathbf{\vec x};\mathbf{\vec \mu},\mathbf\Sigma) =\sqrt{\frac{1}{(2\pi)^{n}det(\mathbf\Sigma)}}\exp\left(-\frac 12(\mathbf{\vec x-\vec \mu})^{T}\mathbf\Sigma^{-1}(\mathbf{\vec x-\vec \mu})\right)\]
$n$ 維正態變數具有下列四條性質：
- $n$ 維正態變數的每一個分量都是正態變數；反之， ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n$ 都是正態變數，且相互獨立， $({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n)$ $n$ 維正態變數
- $n$ 維隨機變 $({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n)$ 服 $n$ 維正態分佈的充要條件 ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n$ 的任意線性組合 $l_1{\mathbf x}_1+l_2{\mathbf x}_2+\cdots+l_n{\mathbf x}_n$ 服從一維正態分佈，其 $l_1,l_2,\cdots,l_n$ 不全為0
- $({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n)$ 服 $n$ 維正態分佈， ${\mathbf y}_1,{\mathbf y}_2,\cdots,{\mathbf y}_k$ ${\mathbf x}_j,j=1,2,\cdots,n$ 的線性函式， $({\mathbf y}_1,{\mathbf y}_2,\cdots,{\mathbf y}_k)$ 也服從多維正態分佈
  這一性質稱為正態變數的線性變換不變性
  - $({\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n)$ 服 $n$ 維正態分佈， ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n$ 相互獨 $\Longleftrightarrow$ ${\mathbf x}_1,{\mathbf x}_2,\cdots,{\mathbf x}_n$ 兩兩不相關

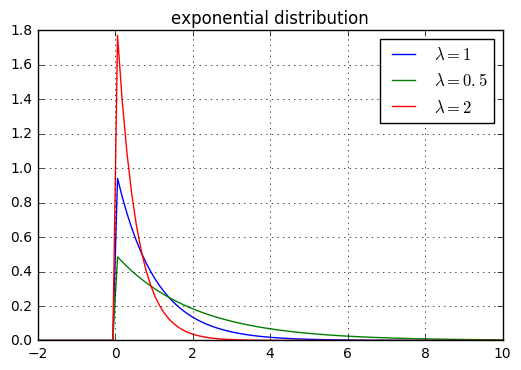
6.4 指數分佈

指數分佈：
- 概率密度函式： \[p(x;\lambda)=\begin{cases} 0,& x\lt0\\ \frac{\lambda}{\exp(\lambda x)},& x\ge0\\ \end{cases} \]
- 期望： $\mathbb E_{\mathbf x}[x]=\frac{1}{\lambda}$
- 方差： $Var_{\mathbf x}[x]=\frac{1}{\lambda^{2}}$

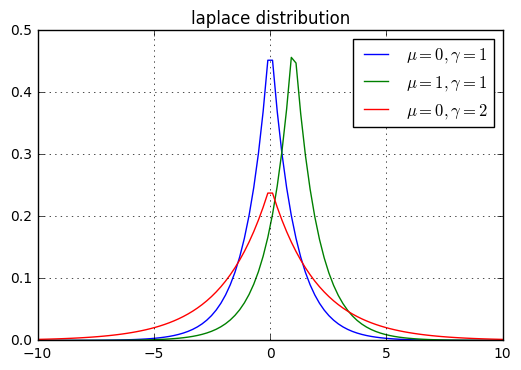
6.5 拉普拉斯分佈

拉普拉斯分佈：
- 概率密度函式： \[p(x;\mu,\gamma)=\frac{1}{2\gamma}\exp\left(-\frac{|x-\mu|}{\gamma}\right) \]
- 期望： $\mathbb E_{\mathbf x}[x]=\mu$
- 方差： $Var_{\mathbf x}[x]=2\gamma^{2}$

6.6 狄拉克分佈

狄拉克分佈：假設所有的概率都集中在一 $\mu$ 上，則對應的概率密度函式為： \[p(x)=\delta(x-\mu) \] 其 $\delta(\cdot)$ 為狄拉克函式，其性質為： \[\delta(x)=0,\forall x\neq 0 \int_{-\infty}^{\infty}\delta(x)dx=1 \]
狄拉克分佈的一個典型用途就是定義連續型隨機變數的經驗分佈函式。假設資料集中有樣 $\mathbf{\vec x}_1,\mathbf{\vec x}_2,\cdots,\mathbf{\vec x}_N$ ，則定義經驗分佈函式： \[\hat p(\mathbf{\vec x})=\frac 1N\sum_{i=1}^{N}\delta(\mathbf{\vec x}-\mathbf{\vec x}_i)\] 它就是對每個樣本賦予了一個概率質 $\frac 1N$ 。
- 對於離散型隨機變數的經驗分佈，則經驗分佈函式就是multinoulli分佈，它簡單地等於訓練集中的經驗頻率。
經驗分佈的兩個作用：
- 通過檢視訓練集樣本的經驗分佈，從而指定該訓練集的樣本取樣的分佈（保證取樣之後的分佈不失真）
- 經驗分佈就是使得訓練資料的可能性最大化的概率密度函式

6.7 多項式分佈與狄裡克雷分佈

多項式分佈的質量密度函式： \[Mult(m_1,m_2,\cdots,m_K;\vec\mu,N)=\frac{N!}{m_1!m_2!\cdots m_K!}\prod_{k=1}^{K}\mu_k^{m_k}\] 它 $(\mu_1+\mu_2+\cdots+\mu_K)^{m_1+m_2+\cdots+m_K}$ 的多項式展開的形式
狄利克雷分佈的概率密度函式： \[Dir(\vec\mu;\vec\alpha)=\frac{\Gamma(\sum_{k=1}^{K}\alpha_k)}{\sum_{k=1}^{K}\Gamma(\alpha_k)}\prod_{k=1}^{K}\mu_k^{\alpha_k-1}\]
可以看到，多項式分佈與狄裡克雷分佈的概率密度函式非常相似，區別僅僅在於前面的歸一化項
- 多項式分佈是針對離散型隨機變數，通過求和獲取概率
- 狄裡克雷分佈時針對連續型隨機變數，通過求積分來獲取概率

6.8 混合概率分佈

混合概率分佈：它組合了其他幾個分量的分佈來組成。
- 在每次生成樣本中，首先通過multinoulli分佈來決定選用哪個分量，然後由該分量的分佈函式來生成樣本。
- 其概率分佈函式為： \[P(\mathbf x)=\sum_{i}P(c=i)P(\mathbf x\mid c=i)\] 其 $P(c=i)$ 為一個multinoulli分佈 $c$ 的取值範圍就是各分量的編號。
前面介紹的連續型隨機變數的經驗分佈函式就是一個混合概率分佈的例子，此 $P(c=i)=\frac 1N$
混合概率分佈可以通過簡單的概率分佈建立更復雜的概率分佈
- 一個常見的例子是混合高斯模型，其 $P(\mathbf x\mid c=i)$ 為高斯模型。每個分量都有對應的參 $(\mathbf{\vec \mu}_i,\mathbf \Sigma_i)$
  - 有些混合高斯模型有更強的約束，如 $\forall i,\mathbf \Sigma_i=\mathbf\Sigma$ ，更進一步還可以要求 $\mathbf\Sigma$ 為一個對角矩陣。
  相關推薦
  
  機器學習數學基礎總結
  
  目錄線性代數一、基本知識本文中所有的向量都是列向量的形式： \[\mathbf{\vec x}=(x_1,x_2,\cdots,x_n)^T=\begin{bmatrix}x_1\\x_2\\ \vdots \\x_n\end{bmatrix}\] 本書中所有的矩 \(\mathbf X\in \
  
  機器學習數學基礎之矩陣理論（三）
  
  gis 引入定義增加 2017年理論值 nbsp 得到正數矩陣求導目錄一、矩陣求導的基本概念 1. 一階導定義 2. 二階導數二、梯度下降 1. 方向導數. 1.1 定義 1.2 方向導數的計算公式. 1.3 梯度下降最快的方向 1.
  
  2—機器學習 - 數學基礎
  
  導數基礎變化 font bsp 分享概率曲線 size 1、夾逼定理 2、導數導數就是曲線的斜率，是曲線的變化快慢的反映 3、泰勒展開應用：數值計算和實踐中的模型簡化 4、方向導數 5、梯度 6、凸函數 7、概率論
  
  【機器學習數學基礎】線性代數基礎
  
  目錄線性代數一、基本知識二、向量操作三、矩陣運算線性代數一、基本知識本書中所有的向量都是列向量的形式： \[\mathbf{\vec x}=(x_1,x_2,\cdots,x_n)^T=\begin{bmatrix}x_1\\x_2\
  
  機器學習數學基礎
  
  泰勒公式泰勒公式： Jensen不等式若f是凸函式，則切比雪夫不等式切比雪夫不等式：切比雪夫不等式的證明過程：大數定理大數定理公式：
  
  機器學習數學基礎001-矩陣及矩陣的基本表示
  
  矩陣及矩陣的基本表示同學們好，我是CSDN學院的講師，講解人工智慧的相關內容，和同學們交流得知，很多同學的數學基礎都不過關，從今天開始就給大家帶來機器學習當中涉及到的相關數學基礎知識。我會近期在微信公眾號(北國課堂)開放一套系列課程，從零開始學機器學習。在公眾號裡面
  
  機器學習數學基礎--偏導數
  
  偏導定義：一個多變數的函式的偏導數是它關於其中一個變數的導數，而保持其他變數恆定（相對於全導數，在其中所有變數都允許變化）。數學表示：函式關於變數x的偏導數寫為或。偏導數符號是圓體字母，區別於全導數符號的正體。由定義可求得：幾何含義：偏導數f'x(x0,y0)
  
  機器學習數學基礎-線性代數
  
  轉載出處：從這篇文章開始，我會寫好一個系列的文章，就叫掌握機器學習數學基礎之XX（重點知識）吧，主要講述在機器學習中主要的一些數學基礎。線性代數為什麼要寫這個系列？網上文章過於全面，一上來就推薦什麼MIT線性代數，推薦各種微積分，推薦什麼《
  
  機器學習數學基礎-優化（上）
  
  掌握機器學習數學基礎之優化[1]（重點知識）是的，你沒有看錯，本來計劃四篇可以寫完的，現在要不止了，優化部分分為一二，一主要是微積分的知識，二主要是約束優化，凸優化，對偶等知識。本來想一篇解決的，但文章之大，一篇放不下.......下面開始分節
  
  機器學習演算法原理總結系列---演算法基礎之(13)模糊C均值聚類（Fuzzy C-means Clustering）
  
  筆者在韓國Chonnam National University攻讀碩士學位，FCM演算法是professer Lim在這學期主要授課的內容，他說他剛發一篇FCM結合遺傳演算法還有各種腦電訊號處理，搭建分析AD病人的EEG訊號的計算智慧模型。反正就是各種難
  
  機器學習演算法原理總結系列---演算法基礎之(11)聚類K均值(Clustering K-means）
  
  一、原理詳解歸類：聚類(clustering) 屬於非監督學習 (unsupervised learning) 無類別標記(class label) 舉例： K-means 演算法： 3.1 Clustering 中
  
  深度學習/機器學習入門基礎數學知識整理（一）：線性代數基礎，矩陣，範數等
  
  前面大概有2年時間，利用業餘時間斷斷續續寫了一個機器學習方法系列，和深度學習方法系列，還有一個三十分鐘理解系列（一些趣味知識）；新的一年開始了，今年給自己定的學習目標——以補齊基礎理論為重點，研究一些基礎課題；同時逐步繼續寫上述三個系列的文章。最近越來越多的
  
  深度學習/機器學習入門基礎數學知識整理（五）：Jensen不等式簡單理解，共軛函式
  
  Jensen不等式及其延伸凸函式最基本的不等式性質，又稱Jensen不等式[1] f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y) 通俗一點講就是，期望的函式值小於等於函式值的期望。
  
  機器學習數學|概率論基礎常見概型分佈期望與方差
  
  機器學習中的數學覺得有用的話,歡迎一起討論相互學習~Follow Me 原創文章,如需轉載請保留出處本部落格為七月線上鄒博老師機器學習數學課程學習筆記概率論對概率的認識,x表示一個事件,則P(x)表示事件發生的概率,其中不
  
  深度學習/機器學習入門基礎數學知識整理（三）：凸優化，Hessian，牛頓法
  
  凸優化理論本身非常博大，事實上我也只是瞭解了一個皮毛中的皮毛，但是對於廣大僅僅想要了解一下機器學習或者深度學習的同學來說，稍微瞭解一點凸優化也就夠了。在實際工程問題中，比如現在我們用的最多的深度神經網路的求解優化問題，都是非凸的，因此很多凸優化理論中非常有價值的
  
  機器學習數學知識積累總結
  
  求解回歸數據 omega 數學需要輸入價格 strong 引子：房價預測給定一組房價數據$x^{(i)},y^{(i)}$,其中x可以是標量scala,也可以是向量，比如可以為房屋面積，還可以包含房屋年齡，地段等信息，y為房屋價格。我們需要找出x和y之間的關系，
  
  深度學習數學基礎介紹（二）概率與數理統計
  
  特征數字特征抽樣分布第5章最大中心 3.4 獨立知識第1章隨機事件與概率§1.1 隨機事件§1.2 隨機事件的概率§1.3 古典概型與幾何概型§1.4 條件概率§1.5 事件的獨立性第2章隨機變量的分布與數字特征§2.1 隨機變量及其分布§2.2 隨機變
  
  機器學習基本概念總結（轉載）
  
  9.png png log images es2017 enter 08-18 機器學習 style 機器學習基本概念總結（轉載）
  
  器學習數學基礎之矩陣理論（二）
  
  pac 本質 uid spa album 空間矩陣 amp .com 目錄一、線性空間 1. 線性空間的概念（1）線性空間的定義（2）線性空間的本質 2. 線性空間的基（1）線性表示（2）線性相關（3）線性無關（4）線性空間基的定義（5）坐標
  
  輕松入門機器學習之概念總結（二）
  
  消息目的作者固定 erp 效率 dev 常用度量歡迎大家前往雲加社區，獲取更多騰訊海量技術實踐幹貨哦~ 作者：許敏接上篇：機器學習概念總結筆記（一） 8）邏輯回歸 logistic回歸又稱logistic回歸分析，是一種廣義的線性回歸分析模型，常用於數據挖掘

機器學習數學基礎總結

線性代數

一、基本知識

二、向量操作

三、矩陣運算

概率論與隨機過程

一、概率與分佈

1.1 條件概率與獨立事件

1.2 聯合概率分佈

二、期望

三、方差

3.1 方差

3.2 協方差與相關係數

3.3 協方差矩陣

四、大數定律及中心極限定理

4.1 切比雪夫不等式

4.2 大數定理

4.3 中心極限定理

五、不確定性來源

六、常見概率分佈

6.1 均勻分佈

6.2 二項分佈

6.3 高斯分佈

6.3.1 一維正態分佈

6.3.2 多維正態分佈

6.4 指數分佈

6.5 拉普拉斯分佈

6.6 狄拉克分佈

6.7 多項式分佈與狄裡克雷分佈

6.8 混合概率分佈

相關推薦