在上一篇文章的最後，我們指出，引數估計是不可能窮盡討論的，要想對各種各樣的引數作出估計，就需要一定的引數估計方法。今天我們將討論常用的點估計方法：矩估計、極大似然估計，它們各有優劣，但都很重要。由於本系列為我獨自完成的，缺少審閱，**如果有任何錯誤，歡迎在評論區中指出，謝謝**！ [TOC] ## Part 1：矩法估計 矩法估計的重點就在於“矩”字，我們知道矩是概率分佈的一種數字特徵，可以分為原點矩和中心矩兩種。對於隨機變數$X$而言，其$k$階原點矩和$k$階中心矩為 $$ a_k=\mathbb{E}(X^k),\quad m_k=\mathbb{E}[X-\mathbb{E}(X)]^k, $$ 特別地，一階原點矩就是隨機變數的期望，二階中心矩就是隨機變數的方差，由於$\mathbb{E}(X-\mathbb{E}(X))=0$，所以我們不定義一階中心矩。 實際生活中，我們不可能瞭解$X$的全貌，也就不可能通過積分來求$X$的矩，因而需要通過樣本$(X_1,\cdots,X_n)$來估計總體矩。一般地，由$n$個樣本計算出的**樣本$k$階原點矩**和**樣本$k$階中心矩**分別是 $$ a_{n,k}=\frac{1}{n}\sum_{j=1}^{n}X_j^k,\quad m_{n,k}=\frac{1}{n}\sum_{j=1}^{n}(X_j-\bar X)^k. $$ 顯然，它們都是統計量，因為給出樣本之後它們都是可計算的。形式上，樣本矩是對總體矩中元素的直接替換後求平均，因此總是比較容易計算的。容易驗證，$a_{n,k}$是$a_k$的**無偏估計**，但$m_{n,k}$則不是。 特別地，$a_{n,1}=\bar X$， $$ m_{n,2}=\frac{1}{n}\sum_{j=1}^{n}(X_j-\bar X)^2=\frac{n-1}{n}S^2\xlongequal{def}S_n^2, $$ 一階樣本原點矩就是樣本均值，二階樣本中心矩卻**不是樣本方差**，而需要經過一定的調整，這點務必注意。這裡也可以看到，由於$S^2$是$\mathbb{D}(X)$的無偏估計，$S_n^2$自然就不是了。 下面給出**矩法估計**的定義：設有總體分佈族$X\sim f(x;\theta)$，這裡$\theta$是引數，$g(\theta)$是引數函式。如果$g(\theta)$可以被表示為某些總體矩的函式： $$ g(\theta)=G(a_1,\cdots,a_k,m_2,\cdots,m_k), $$ 則從$X$中抽取的簡單隨機樣本可以計算相應的樣本原點矩$a_{n,k}$和中心矩$m_{n,k}$，替換掉$G$中的總體矩，就得到**矩估計量**為 $$ \hat g(\boldsymbol{X})=G(a_{n,1},\cdots,a_{n,k},m_{n,2},\cdots,m_{n,k}). $$ 看著很長的一段定義，其實體現出的思想很簡單，就是將待估引數寫成矩的函式，再用樣本矩替換總體矩得到矩估計量。並且實踐中，還可以遵循以下的原則： - **如果低階矩可以解決問題，不要用高階矩**。這是因為低階矩的計算總是比高階矩更容易的。 - **如果原點矩可以解決問題，不要用中心矩**。這是因為中心矩既不好算，還是有偏估計。 運用矩法估計，我們可以很容易地得到一些總體矩存在的分佈的引數點估計。下面舉書上的例子——Maxwell分佈為例，其總體密度為 $$ p(x)=2\sqrt{\frac{\theta}{\pi}}e^{-\theta x^2}I_{x>0}. $$ 現在要對此引數$g(\theta)=1/\theta$作估計。用矩法估計的話，我們要求出總體矩，按照上面的原則，假設$X$服從Maxwell分佈，則 $$ a_1=\mathbb{E}(X)=2\sqrt{\frac{\theta}{\pi}}\int_0^{\infty}xe^{-\theta x^2}\mathrm{d}x=\frac{1}{\sqrt{\pi\theta}}, $$ 顯然有 $$ g(\theta)=\frac{1}{\theta}=a_1^2\pi, $$ 所以其矩估計量為$\hat g_1(\boldsymbol{X})=\pi\bar X^2$，簡單快捷地求出了矩估計量。 但是，矩估計量唯一嗎？我們不妨再往上計算一層，計算其二階原點矩$a_2$，它的計算比$a_1$稍微複雜一些，有 $$ \begin{aligned} a_2&=\mathbb{E}(X^2)=2\sqrt{\frac{\theta}{\pi}}\int_0^\infty x^2e^{-\theta x^2}\mathrm{d}x\\ &=2\sqrt{\frac{\theta}{\pi}}\int_0^\infty -\frac{x}{2\theta}\mathrm{d}(e^{-\theta x^2})\\ &=2\sqrt{\frac{\theta}{\pi}}\int_0^\infty e^{-\theta x^2}\cdot\frac{1}{2\theta}\mathrm{d}x\\ &=\frac{1}{2\theta},\\ g(\theta)&=\frac{1}{\theta}=2a_2, \end{aligned} $$ 從這個角度來看，其矩估計量為$\hat g_2(\boldsymbol{X})=\frac{2}{n}\sum_{j=1}^n X_j^2$。 你不能說哪一種矩估計量錯了，因為它們都是基於矩法計算得到的合理矩估計量，但是$\hat g_1\ne \hat g_2$是顯然的，所以**矩估計量是不唯一的**。另外，由於兩個矩估計量用到的都是原點矩，且次數都是一次，所以它們都是無偏的。這是矩估計的缺點之一——即得到的估計量不唯一，哪一個更好還有待於實踐的選擇。 > 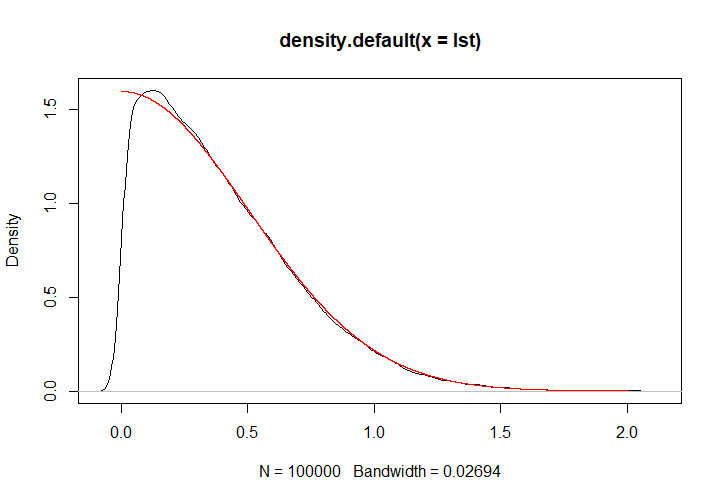現在我們來檢驗一下哪個統計量效果更好一些，假設引數$\theta=2$。為此，我們需要設法從Maxwell分佈中抽樣，抽取100000個樣本，分成50組，每一組包含2000個樣本。 > > 如何從Maxwell分佈中抽樣是一個需要考慮的問題，使用MCMC抽樣法，下面的函式是用於從Maxwell分佈中抽樣的： > > ```R > p <- function(x, theta){ > # Maxwell分佈的密度函式，無正則化因子 > return(exp(-theta*(x^2))) > } > > maxwell <- function(n, theta){ > # 從引數為theta的Maxwell分佈中抽取n個樣本 > buffer <- 10000 > samples <- c() > x <- 1 # 初始值 > for (i in 1:(buffer+n)){ > y <- runif(1, x-0.5, x+0.5) # 極小鄰域 > h <- runif(1) > if (y > 0 && h < p(y,theta)/p(x,theta)){ > x <- y > } > if (i > buffer){ > samples[i-buffer] <- x > } > } > return(samples) > } > ``` > > 此程式是能夠正常執行的，下圖中，黑色為抽樣核密度，紅色為實際的密度曲線。 > > > > 對於2000個一組的樣本，計算其估計量的值，結果如下： > > > > 在樣本容量為2000時，兩個估計量的表現類似，精度都在$\pm 0.1$左右，不能說有多好；但對於我們的100000個樣本，如果一起計算，則 > $$ > \hat g_1(\boldsymbol{X})=0.5000618,\\ > \hat g_2(\boldsymbol{X})=0.499744, > $$ > 效果都不錯。 事實上，$a_{n,k}$總是$a_k$的無偏估計、強相合估計，所以這也成為了矩估計的優點，只要選擇的矩是原點矩的話。但是，我們也可以看到即使樣本容量多達2000，矩估計也偶然會出現20%的較大誤差，因此矩估計的精度是難以解決的痛；並且，矩法估計要求總體矩一定是要存在的，對於柯西分佈這類奇形怪狀的分佈，矩法估計就沒法使用。 ## Part 2：極大似然估計 極大似然估計是另外一種引數點估計的方法，它採用的思路與矩估計的“直接替代”不同。矩估計更像是一種貪圖方便的做法，採用直接替代法而不顧後果，這樣雖然有無偏性和強相合性作為保證，但精度卻無法考慮。極大似然估計源於事情發生的可能性，它總是在可選擇的引數中，選擇**最有可能**導致這個抽樣結果發生的引數，作為引數的估計量。 如何量度這種事情發生的可能性呢？我們以離散情況為例，離散情況下，如果你抽取了一組樣本$\boldsymbol{X}=(X_1,\cdots,X_n)$，它的觀測值是$(x_1,\cdots,x_n)$，則在引數為$\theta$的情況下，這組觀測值發生的概率就是 $$ \mathbb{P}(X_1=x_1,\cdots,X_n=x_n|\theta), $$ 既然不同的$\theta$對應著不同的發生概率，在發生概率和$\theta$之間就存在一個對應關係，這個關係就稱為**似然函式**，記作$L(\theta)$，即 $$ L(\theta)=\mathbb{P}(X_1=x_1,\cdots,X_n=x_n|\theta). $$ 極大似然估計要做的，就是找到一個$\theta$使得$L(\theta)$最大，就這麼簡單。如果對於連續的情況，則用聯合密度函式表示這個聯合概率函式即可。總而言之，極大似然估計的要點，就是先寫出似然函式來，**似然函式與聯合概率函式是形式上一致的**，只是主元從$\boldsymbol{x}$變成了待估引數$\theta$。 依然以Maxwell分佈為例，它的總體密度為 $$ p(x)=2\sqrt{\frac{\theta}{\pi}}e^{-\theta x^2}I_{x>0}. $$ 所以似然函式就是聯合密度函式的形式，寫成 $$ \begin{aligned} L(\theta)&=2^n\left(\frac{\theta}{\pi} \right)^{n/2}\exp\left(-\theta\sum_{j=1}^n x_j^2 \right)I_{x_{(1)}>0}. \end{aligned} $$ 要如何對這個函式求$\theta$的最大值？既然這裡$L(\theta)$是**可導**的，顯然對$\theta$求導最方便，但是對$L(\theta)$求導顯然不太方便，注意到使$L(\theta)$最小的$\theta$值必然也使得$\ln L(\theta)$最小，所以我們完全可以對似然函式的對數求導。這個技巧過於常用，以至於人們直接給似然函式的對數$\ln L(\theta)$起了一個專門的名字：**對數似然函式**，記作$l(\theta)$。由於聯合密度函式是總體密度的乘積，對數似然就是總體密度對數之和，經過降次，求導肯定更容易了。 在這裡， $$ l(\theta)=n\ln 2+\frac{n}{2}\ln\theta-\frac{n}{2}\ln \pi-\theta\sum_{j=1}^n x_j^2+\ln I_{x_{(1)}>0}. $$ 和$\theta$無關的項可以直接視為常數，所以 $$ l(\theta)=C+\frac{n}{2}\ln\theta-\theta\sum_{j=1}^n x_j^2,\\ \frac{\partial l(\theta)}{\partial\theta}=\frac{n}{2\theta}-\sum_{j=1}^n x_j^2. $$ 令這個偏導數為$0$，就得到了$\theta$的極大似然估計量為 $$ \hat\theta_{\text{MLE}}=\frac{n}{2\sum_{j=1}^n X_j^2}. $$ 但是，問題還沒有解決，我們要求的是$(1/\theta)$的極大似然估計，怎麼把$\theta$的極大似然估計給求出來了？其實，參考這裡極大似然估計的來源，只有$\hat\theta_{\text{MLE}}$能讓似然函式的偏導數為$0$取到最大值，由鏈式法則，也只有$1/\hat\theta_{\text{MLE}}$能讓似然函式對$1/\theta$的偏導數為$0$，因此我們得到極大似然估計一個極為有用的性質： - 如果$\hat\theta$是$\theta$的極大似然估計，則$g(\hat\theta)$是$g(\theta)$的極大似然估計。 雖然這裡對$g$有一定的約束，比如$g$可微之類的，但是一般情況下這樣的約束都是可以滿足的。因此，我們得到 $$ \left(\frac{1}{\theta} \right)_{\text{MLE}}=\frac{2}{n}\sum_{j=1}^nX_j^2=\hat g_2(\boldsymbol{X}). $$ 可以看到，它的極大似然估計與矩法估計中，二階矩對應的矩法估計一致。 不過實際上，極大似然估計並沒有這麼一帆風順，有時候$L(\theta),l(\theta)$不一定可導，導數為$0$的點也不一定唯一（這兩種情況一般發生在總體是均勻分佈的時候），這時候要根據似然函式的性質靈活選擇極大似然估計量。 需要注意的是，極大似然估計的無偏性、相合性都是沒法保證的，為什麼我們要使用它呢？原因很簡單：它的原理很好解釋，並且效果確實還不錯。 ## Part 3：一個例題 截尾資料是之前一直被我們忽略的題目，這道題出自習題2的第26題，瞭解這道題還是很有必要的。 某電子元件服從指數分佈$E(1/\lambda)$，密度函式為 $$ f(x)=\frac{1}{\lambda}e^{-\frac{x}{\lambda}}I_{x>0}, $$ 從這批產品中抽取$n$個作壽命試驗，規定到第$r$個電子元件失效時停止試驗，這樣獲得前$r$個次序統計量$X_{(1)}\le X_{(2)}\le \cdots\le X_{(r)}$和電子元件的總試驗時間 $$ T=\sum_{i=1}^rX_{(i)}+(n-r)X_{(r)}. $$ **第一步，證明$2T/\lambda \sim \chi^2_{2r}$，即證明$T\sim \Gamma(r,\lambda)$**。注意到總體服從的分佈是指數分佈，具有無記憶性，這是本題考察的一大知識點，因此作如下變換： $$ Z_i=X_{(i)}-X_{(i-1)},\quad i=1,2,\cdots,n,X_{(0)}=0. $$ 這裡要注意，雖然$X_{(r+1)},\cdots,X_{(n)}$**我們沒有觀測到**，但是它們是切實存在的量。$X_{(1)},\cdots,X_{(n)}$的聯合密度函式為 $$ f(x_{(1)},\cdots,x_{(n)})\frac{n!}{\lambda^n}\exp\left\{-\frac{1}{\lambda}\sum_{j=1}^{n}x_{(j)} \right\}I_{00,\cdots,z_n>0}\\ &=\prod_{j=1}^n\left(\frac{(n+1-j)}{\lambda}\exp\left\{-\frac{n+1-j}{\lambda} z_j\right\}I_{z_j>0}\right)\\ &=\prod_{j=1}^n g_j(z_j), \end{aligned} $$ 這裡 $$ g_j(z_j)=\frac{(n+1-j)}{\lambda}e^{-\frac{n+1-j}{\lambda}z_j}I_{z_j>0}, $$ 所以 $$ Z_j\sim E\left(\frac{n+1-j}{\lambda} \right),\quad j=1,\cdots,n.\\ (n+1-j)Z_j\sim E(1/\lambda),\quad j=1,\cdots,n. $$ 於是 $$ T=\sum_{i=1}^r X_{(i)}+(n-r)X_{(r)}=\sum_{j=1}^r(n+1-j)Z_j\sim \Gamma(r,1/\lambda). $$ **第二步，尋找$\lambda$的極大似然估計量**。由於統計量是樣本的函式，而我們實際上沒有獲得$X_{(r+1)},\cdots,X_{(n)}$的觀測值，因此我們只能用$X_{(1)},\cdots,X_{(r)}$來構造統計量。事實上，我們得出了統計量$T$的分佈，可以驗證$T$是充分的，只要求$(X_{(1)},\cdots,X_{(r)})$的聯合密度，運用我們在[次序統計量](https://www.cnblogs.com/jy333/p/14357993.html)處說到的方法，可以得出（忽略示性函式部分） $$ \begin{aligned} &\quad p(x_{(1)},\cdots,x_{(r)})\\ &=n!p(x_{(1)})\cdots p(x_{(r)})\left(\frac{[1-F(x_{(r)})]^{n-r}}{(n-r)!} \right)\\ &=\frac{n!}{(n-r)!}\frac{1}{\lambda^r}\exp\left\{-\frac{1}{\lambda}\sum_{j=1}^{r}x_{(j)} \right\}\exp\left\{-\frac{n-r}{\lambda}x_{(r)} \right\}\\ &=\frac{n!}{(n-r)!\lambda^r}\exp\left\{-\frac{1}{\lambda}\left[\sum_{j=1}^rx_{(j)}+(n-r)x_{(r)} \right] \right\}\\ &=\frac{n!}{(n-r)!\lambda^r}e^{-\frac{t}{\lambda}}. \end{aligned} $$ 因此$T$是一個充分統計量。下尋找極大似然估計，對數似然函式為 $$ l(\lambda)=\ln\left[\frac{n!}{(n-r)!} \right]-r\ln\lambda-\frac{t}{\lambda}, $$ 這裡引數空間（引數的取值範圍）為$\lambda>0$。對其求偏導，有 $$ \frac{\partial l(\lambda)}{\partial \lambda}=-\frac{r}{\lambda}+\frac{t}{\lambda^2}=0 $$ 所以 $$ \hat\lambda_{\text{MLE}}=\frac{T}{r}. $$ 如果要求指數分佈引數$1/\lambda$的估計量，則利用極大似然估計的可對映性，得到 $$ \widehat{\left(\frac{1}{\lambda}\right)}_{\text{MLE}}=\frac{r}