Problem Description

Many geometry（幾何）problems were designed in the ACM/ICPC. And now, I also prepare a geometry problem for this final exam. According to the experience of many ACMers, geometry problems are always much trouble, but this problem is very easy, after all we are now attending an exam, not a contest :)
Give you N (1<=N<=100) segments（線段）, please output the number of all intersections（交點）. You should count repeatedly if M (M>2) segments intersect at the same point.

Note:
You can assume that two segments would not intersect at more than one point.

Input

Input contains multiple test cases. Each test case contains a integer N (1=N<=100) in a line first, and then N lines follow. Each line describes one segment with four float values x1, y1, x2, y2 which are coordinates of the segment’s ending.
A test case starting with 0 terminates the input and this test case is not to be processed.

Output

For each case, print the number of intersections, and one line one case.

Sample Input

2
0.00 0.00 1.00 1.00
0.00 1.00 1.00 0.00
3
0.00 0.00 1.00 1.00
0.00 1.00 1.00 0.000
0.00 0.00 1.00 0.00
0

Sample Output

1
3

Author

lcy

思路

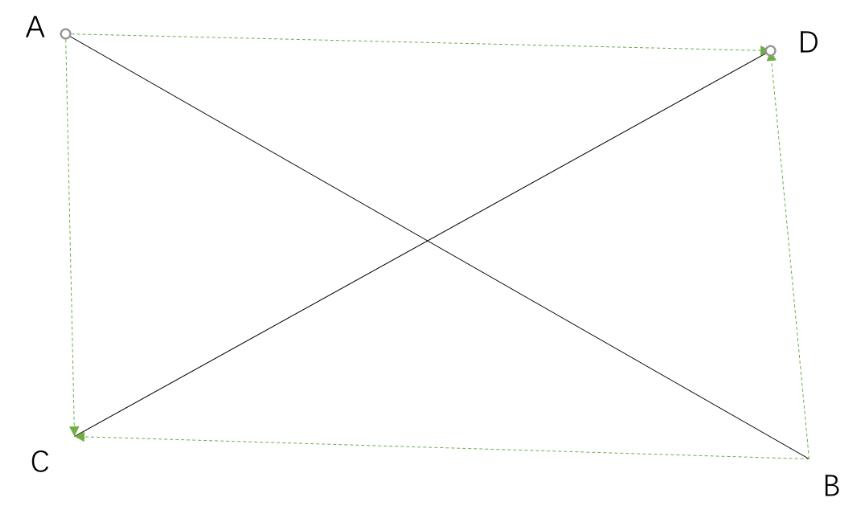
如圖所示，只要\((AC*AD)(BC*BD)<=0\)，\((CA*CB)(DA*DB)<=0\)，利用叉乘性質，兩者必定異號，當兩條直線重合的時候取等

程式碼

#include<bits/stdc++.h>
using namespace std;
struct point
{
    double x,y;
};
struct segment
{
    point s,e;
}a[110];

double crossMult(point a,point b,point c)
{
    return (a.x-c.x)*(b.y-c.y) - (b.x-c.x)*(a.y-c.y);
}

int main()
{
    int n;
    while(cin>>n)
    {
        if(n==0) break;
        for(int i=1;i<=n;i++)
            cin >> a[i].s.x >> a[i].s.y >> a[i].e.x >> a[i].e.y;
        
        
        int ans = 0;
        for(int i=1;i<=n-1;i++)
            for(int j=i+1;j<=n;j++)
            {                         
                double t1 = crossMult(a[j].s, a[j].e, a[i].s);
                double t2 = crossMult(a[j].s, a[j].e, a[i].e);
                double t3 = crossMult(a[i].s, a[i].e, a[j].s);
                double t4 = crossMult(a[i].s, a[i].e, a[j].e);
                if(t1*t2 <= 0 && t3*t4 <= 0) ans++;
            }
        cout << ans << endl;
    }
    return 0;               
}