題目：

Farm Irrigation

Problem Description

Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.

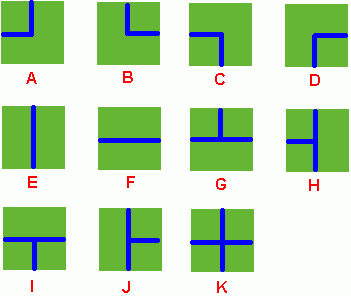
Figure 1

Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map

ADC
FJK
IHE

then the water pipes are distributed like

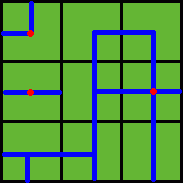
Figure 2

Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.

Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?

Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.

Input

There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.

Output

For each test case, output in one line the least number of wellsprings needed.

Sample Input

2 2 DK HF 3 3 ADC FJK IHE -1 -1

Sample Output

2 3

題目描述：

         時隔一段時間再寫這道題又有了新的收穫，看自己以前寫的程式碼真的是有感觸，

 有圖中幾種形狀的水管，給出一個n*m的矩陣，問最少需要多少水源點可以使整個圖有水流通。

 一個搜尋獨立子圖的問題，有意思的是水管形狀各種各樣，只有介面關聯才可以流通，以前我寫的是把各個水管的情況用if一一列舉，然後搜尋，這次學聰明瞭，用的二維陣列儲存的水管形狀。要方便很多。

解題程式碼：

#include<stdio.h> #include<string.h> int a,b; char d[110][110]; int bo[110][110]; int qw[15][4] = { {1,1,0,0},{0,1,1,0},{1,0,0,1}, {0,0,1,1},{0,1,0,1},{1,0,1,0}, {1,1,1,0},{1,1,0,1},{1,0,1,1}, {0,1,1,1},{1,1,1,1} }; int next[4][2] = {0,-1, -1,0, 0,1, 1,0}; void dfs(int x,int y) { int tx,ty,i; if(bo[x][y]) return ; bo[x][y] = 1; for(i=0;i<4;i++){ tx = x + next[i][0]; ty = y + next[i][1]; if(tx >= 0 && tx < a && ty >= 0 && ty < b){ if(qw[d[x][y] - 'A'][i] && qw[d[tx][ty] - 'A'][(i + 2)%4]) //如果介面關聯則搜尋 dfs(tx,ty); } } return ; } int main() { int i,j; while(scanf("%d%d",&a,&b), a >= 0 && b >= 0){ memset(d,'\0',sizeof(d)); memset(bo,0,sizeof(bo)); for(i = 0 ;i < a;i ++) scanf("%s",d[i]); int t; for(t = i = 0 ;i < a;i ++){ for(j = 0;j < b;j ++){ if(!bo[i][j]){ t ++; dfs(i,j); } } } printf("%d\n",t); } return 0; }