什麼是黎曼和?什麼是定積分?
在初等數學中學習了三角形,四邊形,多邊形的面積計算:

現在來學習 的面積是如何定義的,以及如何計算的:

1 拋物線下的曲邊梯形
1.1 問題
之前介紹過,要求 ,
之間的曲邊梯形的面積
:

可以把 均分為
份,以每一份線段為底,以這一份線段的右側的函式值為高做矩形:

當 的時候,矩形面積和就是曲面下的面積:

那麼,能不能以這一份的線段的左側的函式值為高做矩形?

1.2 計算
算一算就知道了。先把 均分成
份,每份長為
,以及各個劃分點的座標如下:

把座標組成兩個集合:
因此,以左側的函式值為高的矩形和可以如下計算:

同樣的道理,可以得到以右側的函式值為高的矩形和:

當 的時候,兩者是相等的,它們都是曲邊梯形的面積:
2 狄利克雷函式的曲邊梯形
之前介紹連續的時候就介紹過狄利克雷函式:
也見識過它的古怪性質。這裡也要把它拉出來作一個反面典型。 的影象是沒有辦法畫的,非要畫也就是這樣的:

假設要求 內的曲邊梯形面積,嘗試對
進行
等分,那麼等分點必然為有理數點(下圖為了演示方便,調整了下
座標的比例):

所以這些等分點的函式值必然為1。以1為高,以等分割槽間長度為底作矩形,可以得到:

這些矩形的和必然為1,可以想象進行 等分也依然為1,所以有:
下面換一種劃分方式,以鄰近的兩個無理數作為端點劃分區間,這些區間的端點的函式值必然為0,以區間長度為底,0為高,得到的矩形和為:
可見,對於 而言,不同的劃分區間、不同的高的取法,會導致不同的矩形和:
3 黎曼和

格奧爾格·弗雷德里希·波恩哈德·黎曼(1826-1866)是德國數學家,黎曼幾何學創始人,複變函式論創始人之一。在數學界搞風搞雨的黎曼猜想也是他的傑作。
基於對剛才兩種情況:
-
拋物線下的曲邊梯形
-
狄利克雷函式下的曲邊梯形
的思考,看到不同劃分帶來的效果,黎曼先發明瞭黎曼和,進而定義了曲邊梯形的面積,也就是定積分。
3.1 任意劃分
不一定需要均分為
份,可以任意分割:

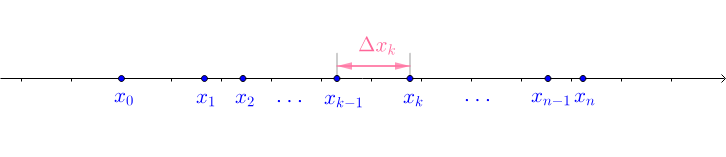
很顯然用於分割區間的點符合:
令 ,那麼集合:
稱為 的一個
。劃分
定義了
個子區間:
稱為第
個子區間,更一般的
被稱為第
個子區間:

第 個子區間的長度為
:
3.2 任意高度
對於某一個劃分 ,在其第
個子區間內隨便選一個數
:

以 作為矩形的高:

那麼矩形的高度也可以是任意的:
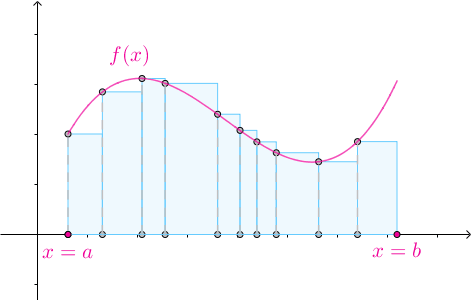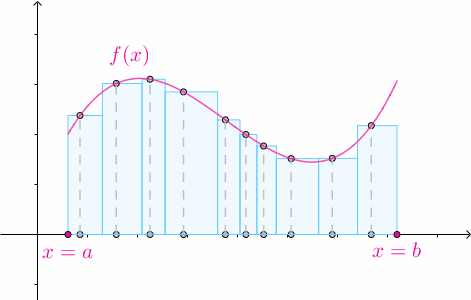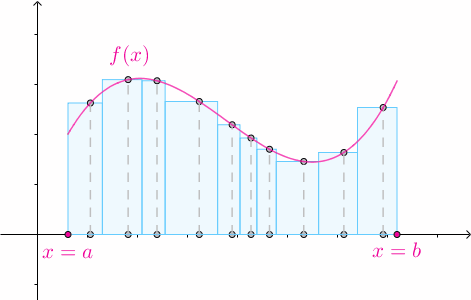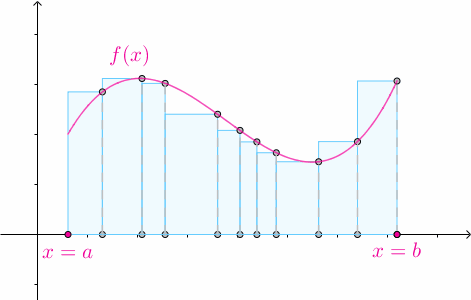
3.3 黎曼和
根據剛才的講解,可以得到如下定義:
設函式在
上有定義,在
上任意插入若干個分點:
這些分點的集合:
稱為
的一個
。劃分
定義了
個子區間:
它們的長度依次為:
在每個子區間
上任取選取一個數
,以
為底,
為高構造矩形,這些矩形的和:
稱為
在
上的
。
之前計算的 、
是黎曼和:

狄利克雷函式中劃分出來的矩形和 、
也是黎曼和。
4 定積分
隨著 的劃分不斷變細,所有子區間的長度趨於0時,黎曼和不斷地逼近曲邊梯形的面積:

這個過程的嚴格化如下:
設函式在
上有定義,對於
上的任意劃分
,
為子區間
上任意選取的數,子區間
的長度為
,記:
如果下述極限存在:
則稱
在
上
,
為
,
為
,
為
在
上的
,
為
,可以標記如下:
回到之前討論的問題:
-
拋物線下的曲邊梯形:
,以及各種劃分都相等,所以
存在,可積
-
狄利克雷函式下的曲邊梯形:
,所以
不存在,不可積
這裡新引入的積分符號是萊布尼茲創造的:
其中, 代表英文中的求和(“sum”),拉長的
則表明積分是和的極限(“limits of sums”)。這個符號相當精練,可以表達非常豐富的資訊:

最新版本(可能有不定期更新):黎曼和與定積分
