## 【OI向】快速傅立葉變換(Fast Fourier Transform) ### FFT的作用 ​ 在學習一項演算法之前,我們總該關心這個演算法究竟是為了幹什麼。 ​ （以下應用只針對OI） ​ 一句話:求多項式乘法(當然它的實際用處很多) ​ 設多項式 ​ $A(x)=a_0+a_1x+a_2x^2+\ldots+a_nx^n$ ​ $B(x)=b_0+b_1x+b_2x^2+\ldots+b_mx^m$ ​ 我們想求 $F(x)=A(x)B(x)=\sum\limits_{i=0}^n\sum\limits_{j=0}^ma_ib_jx^{i+j}$ ​ 肉眼可見的複雜度$O(nm)$ ​ 而使用一般的FFT則複雜度能夠在$O(nlogn)$ （實則帶比較大的常數,但資料範圍大時肯定比$O(nm)$好） ​ 寫這篇部落格是為了讓自己和看到的人能夠梳理一遍FFT這個演算法。 ​ 以下FFT的實現使用比較常見的複數單位根做法。 ### 前置知識 ​ 首先要知道複數是什麼,高中選修即有,網上資料也很多,不贅述,這裡只講FFT直接相關。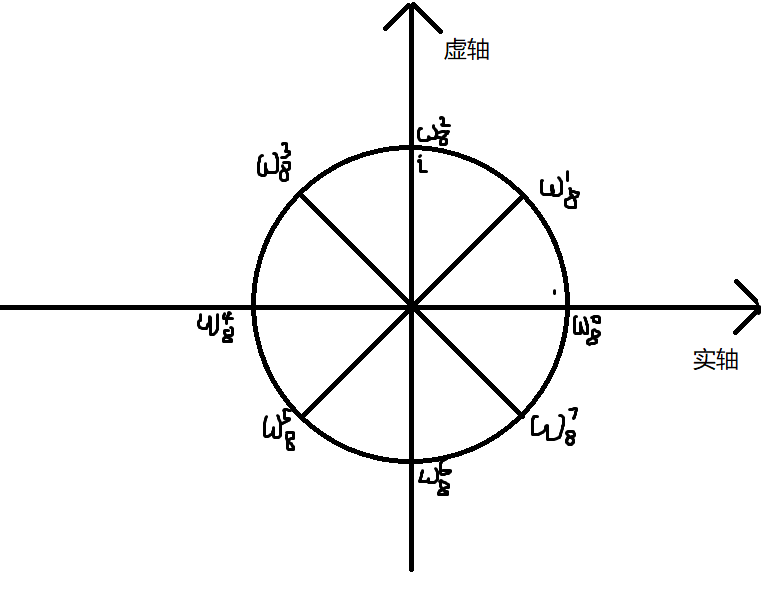 #### 1 複數單位根 ​ 定義: $z^n=1$ 那麼 $z$ 就是n次的單位根 ​ 對於一個$n$次單位根,就是將複數單位圓等分成$n$份,每個數 $w_n^k (k\in[0,n-1) )$ 就被稱作n次的第k個單位根 ​ 如圖 ​  圖中表示了所有8次單位根,其中$w_8^0=1,w_8^1=1+i,w_8^2=i,w_8^3=-1+i\ldots$ 所謂單位根就是這些複數,它們的平方均為1。 **雖然單位根的次數$n$在定義上可以取全體正整數,但是我們在FFT中只需要考慮n為2的整數次冪,以方便我們利用性質。** 單位根有一些性質,我們先列出來看看 （**下邊的n均為2的整次冪!**） ###### 0 單位根乘法 ​ $w_n^i\times w_n^j=w_n^{i+j}$,這個性質實際上不能叫性質,從複數乘法,輻角的概念出發即能夠得證。 ###### 1 消去引理 ​ $w_{2n}^{2k}=w_n^k$ ​ 理解,可以看到 $2k$ 和 $k$ 在 $2n$ 和 $n$ 中佔的比例是相同的,聯想單位圓即可($w_8^2$顯然等於$w_4^1$,均為1) ###### 2 折半引理 ​ 我看了好幾篇部落格,包括知乎,對摺半引理的說法是: 對於 $n$ 等於 $2$ 的整次冪, $w_n^k$經過平方可以得到所有$w_{\frac{n}{2}}^k$(單純來說只需要$n$是二的倍數就好) ​ 兩個小性質都可以證明 ​ $w_n^{2k}=w_{\frac{n}{2}}^k$ ​ 由消去引理,這個小性質是顯然的。從這個性質出發,如果 $k$ 取遍$[0,n-1]$,那麼首先右邊是全了,對於左邊,$2k\in[0,2n-2]$,經歷了一次迴圈, (按道理這裡需要指出一個迴圈性質,但我覺得沒必要) $w_n^{k+n}=w_n^{k}\times w_n^{n}$, 而$w_n^n$即$w_n^0=1$,所以 $2k$ 過了$n-1$之後會經過$\frac{n}{2}$個相同的點 ​ $w_n^k=-w_n^{k+\frac{n}{2}}$ ​ 旋轉$180^\circ$ 事情變得顯然;從複數乘法的角度來說也可以：$w_n^{k+\frac{n}{2}}=w_n^k\times w_n^{\frac{n}{2}}$,而$w_n^{\frac{n}{2}}$恰好為$-1$。 ​ 那麼這個性質告訴我們前一半$k\in[0,\frac{n}{2}-1]$和後一半 $k\in[\frac{n}{2},n-1]$的平方是一樣的,所以同理,兩半的平方值是一樣的,也就是兩部分平方只確定了$\frac{n}{2}$個值,那麼利用前邊第一個小性質,我們不需要迴圈性質就能夠證明折半引理。 ​ 折半引理告訴我們,如果知道了n的所有單位根,那麼$\frac{n}{2}$的單位根我們可以知道,反之,我們利用第二個性質也可以從$\frac{n}{2}$的所有單位根,加一個負號,就能推出所有的 $n$ 次單位根。 ###### 3 求和引理 ​ $\sum\limits_{i=0}^{n-1}w_n^k=0$ ​ 從折半引理看,我們把 $w_n^k$ 分成兩部分$w_n^a (a\in[0,\frac{n}{2}-1] ),w_n^b(b\in[\frac{n}{2},n-1])$,也就是圓的上半部分和下半部分,對應有每個$w_n^a+w_n^b=0$，實際上是$w_n^a+w_n^{a+\frac{n}{2}}=0$,所以兩部分的累加和就是0(**我們上邊已經假設n是2的整次冪了,所以一定是相同大小的兩部分**) #### 單位根的表示 ​ 首先簡單說一下輻角,在複數平面上,從實數軸正半軸逆時針旋轉到複數$z$到原點的連線,中間經過的角度就叫做輻角(大小在$2\pi$之內) ​ 從圓的知識類比一下,我們可以知道 ​ 在敘述 $n$ 次單位根這件事情的時候,我們是將複數單位圓 $n$ 等分之後得到單位根,這樣來看的話,顯然$w_n^1$的輻角是 $\theta=\frac{2\pi}{n}$, 那麼$w_n^k=(w_n^1)^k$ ,那麼$w_n^k$的輻角就是 $k\theta$,我們知道在普通二維平面上單位圓上的點表示為$(cos\theta,sin\theta)$,類比到複平面,就會得到 $w_n^k=cos\theta+sin\theta\ i \ \ \ \ (\theta=\frac{2\pi}n)$ ​ 至此,我們已經瞭解單位根的性質及其表示,然而我們還不知道為什麼要介紹這麼一個東西。下面我們會了解的。 #### 2 多項式的點值表示法及其點值表示法的乘法 ​ 一開始,我們做介紹時設了兩個多項式 ​ $A(x)=a_0+a_1x+a_2x^2+\ldots+a_nx^n$ ​ $B(x)=b_0+b_1x+b_2x^2+\ldots+b_mx^m$ ​ 仔細看的話,我們發現這兩個多項式像什麼?沒錯，像函式,實際上它完全可以當成一個函式表示式。 ​ 即$y=A(x)$ ​ 我們知道,求解一次函式只需要知道兩個點的座標,求解二次函式只需要知道三個點的座標,那麼我們可以換個說法,兩個點確定了一個一次函式,三個點確定了一個二次函式,同樣的,我們可以說 $n+1$ 個點確定了一個 $n$ 次函式,確定的方法很簡單,我們帶入聯立即可(想想我們是怎麼通過兩個點確定一條直線的)。 ​ 現在我們把名詞換一下,”函式“變成“多項式”,就可以改成說 $n+1$ 個不同點確定一個 $n$ 次多項式。 ​ 即點集$((x_0,y_0),(x_1,y_1),\ldots ,(x_n,y_n))$ 能夠確定一個 $n$ 次多項式。 ​ 代入$y=A(x)$看的形象一點 ，我們解下邊的方程組(點是我們已知且在函式上的),就能夠求出來所有的係數 $a$ (就是和求函式解析式一樣的概念),如果用高斯消元來解這樣一個方程組,複雜度是 $O(n^3)$的，這個過程被稱作離散傅立葉逆/反變換(IDFT) 。 $$ \begin{cases} y_0=a_0+a_1x_0+a_2x_0^2+\ldots+a_nx_0^n \\ y_1=a_0+a_1x_1+a_2x_1^2+\ldots+a_nx_1^n\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ y_n=a_0+a_1x_n+a_2x_n^2+\ldots+a_nx_n^n \end{cases} $$ ​ 同時,如果我們知道一個多項式的係數表示式,我們只需要隨便找$n+1$個點 $x$ 代入到$A(x)$中,就可以得到所有的$y$。 ​ 這樣我們就可以將一個多項式從係數表示式 $O(n^2)$ 的轉換成點值表示式。 ​ 把多項式的係數表示換成點值表示的變換被稱作離散傅立葉變換(DFT)。(~~不小心先介紹了逆變換~~) ​ 點值表示式之間想要確定新的點值表示式,只用將y相乘即可($x$對應相等),比如說 ​ $A=((x_0,y_0),(x_1,y_1)\ldots,(x_n,y_n))$ ​ $B=((x_0,y_1'),(x_1,y_2')\ldots,(x_n,y_n') )$ ​ $F=AB=((x_0,y_1y_1'),(x_1,y_2y_2'),(x_2,y_2y_2')\ldots,(x_n,y_ny_n') )$ ​ 因為我們的每個$y_iy_i'$都是一次多項式乘法的結果,按照定義,$F(x_k)=A(x_k)B(x_k)=y_ky_k'=\sum\limits_{i=0}^n\sum\limits_{j=0}^ma_ib_jx_k^{i+j}$我們的多項式乘法本身是隻關心繫數的,和 $x$ 無關(就像函式表示式$y=f(x)$只和各項係數有關而與具體的點無關一樣),而根據我們點值表示法的定義 $y_k=F(x_k)$，所以$(x_0,y_1y_1')$就是$F(x)$上的一個點 $(x_k,F(x_k))$ ​ 一個小問題 一開始我們知道,多項式$A(x)B(x)$的結果理應得到最高次項為$n+m$的$F(x)$,而A，B的直接轉化的點值表示法分別只有$n$個點和$m$個點，最後要真正確定$F(x)$,需要 $n+m+1$個點怎麼辦？好辦,我們一開始把A和B多算一些y,補若干個點補到$n+m+1$個點,多一些點並不會影響什麼,而這樣就能夠創造出$n+m+1$個能夠確定$F(x)$的點集了。 ​ AB的運算得到的新點集,就能夠確定新的 多項式 $F(x)$ 。而在已知 $y_i$和 $y_i'$ 的情況下，運算AB需要的複雜度是 $O(n)$的！ ### 快速傅立葉變換(FFT) ​ 從前置知識點值表示法的內容中,我們可以得到一種新的求多項式 $F(x)=A(x)B(x)$ 的方法 1. ​ DFT,將$A(x)$ $B(x)$ 通過離散傅立葉變換 (DFT)轉化為點值表示法,為了能夠真正確定$F(x)$，A和B都要轉化為$n+m+1$個點以確定最高次項為$n+m$的$F(x)$,複雜度 $O(n^2)$ 2. ​ 將$A(x)$的所有點值和$B(x)$的所有點值對應相乘,得到$F(x)$的點值表示法。複雜度 $O(n)$ 3. ​ IDFT,以所有 $x$ 的各個次項做係數矩陣(以$x_i^1,x_i^2\ldots$做係數矩陣),進行高斯消元,得到$F(x)$的所有係數。複雜度 $O(n^3)$ ~~非常漂亮啊!!我們一通操作,直接得到一個O(n³)的做法能夠進行多項式乘法！！秒！~~ 我們進行這麼多操作,研究了點值表示法能夠對應多項式的係數表示法的事實,當然不是為了花裡胡哨得到一個$O(n^3)$的做法 這個時候,我們就要考慮優化了,優化什麼呢？我們不忍心點值表示運算明明已經達到了極優秀的$O(n)$,而DFT和IDFT卻嚴重拖慢執行。 這個時候,我們就要用到複數單位根了。 ​ 平時我們做函式之類的事情,通常規定 $x\in R$ 實際上我們可以擴充套件數域, 使得 $x\in C$ 即讓$x$從實數擴充套件到整個複數域,作為一個橫座標來使用。然後我們考慮將DFT的過程中任選的$x$,變成有規律的複數單位根,為了使得這些 $x$ 有規律我們還規定,對於一個$n-1$次多項式,我們向多項式 $A(x)$ 和$B(x)$ 代入所有的單位根,即代入所有的 $w_n^k$ ,而所有的單位根是不同的複數,所以點集$(w_n^k,A(w_n^k))$ 就能夠作為$A(x)$的點值表示法,$B(x)$同理。 ​ 接下來我們將 $n$ 次單位根代入到我們的多項式中,為了使用我們上邊指出過的複數單位根的性質,以及為了能夠唯一確定我們的目標多項式,我們選擇的 $n$ 應當是2的整次冪,並且它要大於等於n+m+1。 ​ 代入之後 $A(x)=((w_n^0,A(w_n^0),),(w_n^1,A(w_n^1))\ldots,(w_n^{n-1},A(w_n^{n-1}))$,考慮如何快速求出每個$A(w_n^k)$，我們從消去引理知道,只要知道偶數項的$w_n^k=w_\frac{n}2^{\frac{k}2}$,這提示我們需要將原來的表示式進行一波奇偶分組,從係數表示式入手,現在$A(x)$是一個$n-1$次多項式。 $$ A(x)=(a_0+a_2x^2+a_4x^4+\ldots+a_{n-2}x^{n-2})+(a_1+a_3x^3+\ldots+a_{n-1}x^{n-1})\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =(a_0+a_2x^2+a_4x^4+\ldots+a_{n-2}x^{n-2})+x(a_1+a_3x^2+a_5x^4+\ldots+a_{n-1}x^{n-2})\\ $$ ​ 設$A_1(x)=(a_0+a_2x+a_4x^2+\ldots+a_{n-2}x^{\frac{n}2-1}),A_2(x)=(a_1+a_3x+\ldots+a_{n-1}x^{\frac{n}2-1})$ ​ 我們會得到$A(x)=A_1(x^2)+xA_2(x^2)$ ​ 將所有$x$ 寫成單位根的樣子 $$ \begin{aligned} A(w_n^k)& =a_0+a_1w_n^k+a_2w_n^{2k}+a_3^{3k}+\ldots+a_{n-1}w_n^{(n-1)k} \\&=A_1(w_n^{2k} )+w_n^kA_2(w_n^{2k} )\\ &=(a_0+a_2w_n^{2k}+a_4w_n^{4k}+\ldots+a_{n-2}w_n^{(n-2)k})+w_n^k(a_1+a_3w_n^{2k}+\ldots+a_{n-1}^{(n-2)k})\\&=(a_0+a_2w_\frac{n}2^k+a_4w_\frac{n}2^{2k}+\ldots+a_{n-2}w_\frac{n}2^{(\frac{n}2-1)k})+w_n^k(a_1+a_3w_\frac{n}2^{k} +\ldots+a_{n-1}^{(\frac{n}2-1)k})\\ &=A_1(w_\frac{n}2^k)+w_n^kA_2(w_\frac{n}2^k) \end{aligned} $$ ​ 對於$k\in[0,\frac{n}2-1]$，$A(w_n^k)=A_1(w_\frac{n}2^k)+w_n^kA_2(w_\frac{n}2^k)$ ​ 對於$k\in[\frac{n}2,n-1]$, 從$w_n^k=-w_n^{k+\frac{n}{2}},w_n^k=w_\frac{n}2^\frac{k}2$由於$k$已經大於$\frac{n}2$,所以這裡所有的$A_1(w_\frac{n}2^k)=A_1(w_\frac{n}2^{k-\frac{n}2})$,$A_2$同理 ​ 所以$A(w_n^k)=A_1(w_{\frac{n}2}^{k-\frac{n}2})-w_n^{k-\frac{n}2}A_2(w_{\frac{n}2}^{k-\frac{n}2})$ 也就是我們可以直接引用在前一半已經算出來過的$A_1A_2$,來計算出後一半的所有$A(w_n^k)$ ,這樣我們把計算的規模縮小了一半,同理,我們要知曉前一半$A_1$和$A_2$的值,也可以從一半的前一半推之,即遞迴便可以求解,最後需要進行log層計算,然後只需要在遞迴的底層對一個點進行 $O(n)$ 的多項式運算然後每層$O(n)$的向上合併,最終的複雜度是 $T(n)=2T(\frac{n}2)+O(n)$ 其最終複雜度是$O(nlogn)$的。這樣我們通過將多項式拆分成兩部分然後進行相似性的遞迴,使得我們的DFT能夠在$O(nlogn)$ 的複雜度下得到多項式的點值表示式,這個過程就被稱作FFT。 ### 快速傅立葉逆變換（IFFT） ​ 如何快速的把得到的點值表示法的多項式變成係數表示法,先放一個結論吧 $$ 有多項式\ F(x)=\sum\limits_{i=0}^{n-1}f_ix^i\\ 那麼多項式的點值表示法就是((w_n^0,F(w_n^0)),(w_n^1,F(w_n^1)),\ldots,(w_{n}^{n-1},F(w_n^{n-1})) ) \\則每個多項式的係數 f_k=\frac{1}n\sum\limits_{i=0}^{n-1}y_iw_n^{-ki} $$ ​ 也就是說,如果我們知道了一個多項式,可以用FFT化作點值表示,而如果我們知道了所有點值反過來求所有係數,我們發現求每個係數的形式和求每個點值的形式是相同的不同的是多了一個係數$\frac{1}n$以及在$w$上標多了一個負號,而這是不影響單位根的三項引理的,也就說,這個反向的過程依然可以用FFT解決。如此一來,我們就可以同樣的在$O(nlogn)$ 的複雜將點值表示轉化為係數表示。 ​ 關於IFFT的證明: ​ 我們把每個點展開成多項式,即把$(w_n^k,A(w_n^k) )$還原成多項式的模樣然後以多項式的係數作為列向量相乘,就能夠得到所有的點值$y$ $$ \begin{bmatrix} &1,&(w_n^0)^1,&(w_n^0)^2,&\ldots,&(w_n^{0})^{n-1}\\ &1,&(w_n^1)^1,&(w_n^1)^2,&\ldots,&(w_n^1)^{n-1}\\ &&&\vdots\\ &1,&(w_n^{n-1})^1,&(w_n^{n-1})^2,&\ldots,&(w_n^{n-1})^{n-1}) \end{bmatrix} \begin{bmatrix} a_0\\a_1\\a_2\\\vdots\\a_{n-1} \end{bmatrix}= \begin{bmatrix} y_0\\y_1\\y_2\\\vdots\\y_{n-1} \end{bmatrix} $$ ​ 我們的點值表示法所得到的矩陣是一個範德蒙矩陣,而我們進行IFFT的過程就是已知向量 $y$ 以及點矩陣$W$ 求向量$a$ ​ 那麼我們只需要計算 $yW^{-1}$ 即可,對於這個範德蒙矩陣求逆。 ​ 直接構造矩陣S $$ \begin{bmatrix} &1,&(w_n^{-0})^1,&(w_n^{-0})^2,&\ldots,&(w_n^{-0})^{n-1}\\ &1,&(w_n^{-1})^1,&(w_n^{-1})^2,&\ldots,&(w_n^{-1})^{n-1}\\ &&&\vdots\\ &1,&(w_n^{-(n-1)})^1,&(w_n^{-(n-1)})^2,&\ldots,&(w_n^{-(n-1)})^{n-1}) \end{bmatrix} $$ ​ 根據求和引理,$c_{i,j}=w_{i,k}s_{k,j}$兩個矩陣相乘就會得到矩陣C $$ \begin{bmatrix} &n,&0,&0,&\ldots,&0\\ &0,&n,&0,&\ldots,&0\\ &&&\ddots\\ &0,&0,&0,&\ldots,&n \end{bmatrix} $$ ​ 這個矩陣乘上一個$\frac{1}n$就是單位矩陣,所以以$w_n^{-k}$作為點的橫座標依次代入矩陣再乘一個$\frac{1}n$就是我們需要的$W^{-1}$,所以只需要我們再用$w_n^{-k}$做一遍FFT,將結果乘$\frac{1}n$即可。 ​ 這樣一來,我們用點值表示法就能夠$O(nlogn)$快速求出係數表示了。 ### 蝴蝶變換 ​ 蝴蝶變換是FFT的一個優化,之所以要優化,是因為純遞迴求解FFT效率並不高,所以考慮如何迭代求解。 ​ 每次奇偶分組的時候,我們都會挑一個當前所在位置編號$i$ 為偶數的分到左邊,為奇數的分到右邊。 ​ 偶數的偶數的偶數次項到最後,就會是0,多一個奇數就會在頭多1...（感性理解） ​ 總之從變換的規律來看,我們遞迴到最後,係數的分組是原來係數的二進位制反轉 ​ 比如我們有一個7次多項式,有8項係數$a_0-a_7$ ​ 分組得到的就是 $$ \begin{matrix} 0,1,2,3,4,5,6,7\\ 0,2,4,6,1,3,5,7\\ 0,4,2,6,1,5,3,7\\ 0,4,2,6,1,5,3,7\\ 二進位制表示下就是\\ 000,001,010,011,100,101,110,111\\ 000,010,100,110,001,011,101,111\\ 000,100,010,110,001,101,011,111\\ 000,100,010,110,001,101,011,111 \end{matrix} $$ ​ 你看最後一組的分配,就是每個數二進位制反轉的結果。 ​ 換言之,我們一開始如果將係數二進位制反轉,然後從下往上推,每次都能推出一個長度更長的多項式,這樣子問題就可以一步步向上推出全域性的答案。 ​ 終於,我們得到了整個FFT的演算法(~~typroa顯示共4862詞(不包括下邊的程式碼),碼了一天,淦~~)！下面會在例題裡貼上一個模板,然後隨著做題會更新一些題目總結吧。 ####資料參考 ： [【學習筆記】超簡單的快速傅立葉變換（FFT）（含全套證明）](https://blog.csdn.net/weixin_45697774/article/details/111710443) [單位根-百度百科](https://baike.baidu.com/item/%E5%8D%95%E4%BD%8D%E6%A0%B9) [OIwiki(~~裡邊還有較詳細的二進位制反轉證明,我懶了不想寫了~~)](https://oi-wiki.org/math/poly/fft/#_9) [百度上的傅立葉變換(~~主要看嚴謹概念來的,然鵝看不大懂,然後題目就多了個【OI向】~~)](https://baike.baidu.com/item/%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2/7119029?fr=aladdin) [學校的非公開資料]這個就莫得連線 ## 例題 ​ [【模板】多項式乘法（FFT）](https://www.luogu.com.cn/problem/P3803) ​ 程式碼如下：

點選此處展開和收起程式碼

```cpp #include #define reg register typedef long long ll; using namespace std; inline int qr(){ int x=0,f=0;char ch=0; while(!isdigit(ch)){f|=ch=='-';ch=getchar();} while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} return f?-x:x; } const int maxn=3e6+199; const double PI=3.14159265358979; int n,m; struct Complex{ double x,y; Complex operator+(const Complex &t)const { return (Complex){x+t.x,y+t.y}; } Complex operator-(const Complex &t)const{ return (Complex){x-t.x,y-t.y}; } Complex operator* (const Complex &t)const { return (Complex){x*t.x-y*t.y,x*t.y+y*t.x}; } }a[maxn],b[maxn]; int rev[maxn],bit,tot;//反轉的二進位制數 void fft(Complex c[],int inv){//inv表示的是單位根轉動的方向 for(reg int i=0;i>1]>>1)|((i&1)<<(bit-1));//記錄每個數的二進位制反轉 } //rev記錄的是每個二進位制數的二進位制逆轉,我們這個遞推是求出來除去第0位的逆再把第0位放到最高位,就能夠得到這個數的逆 fft(a,1),fft(b,1);//轉化為點 for(reg int i=0;i